题目内容
数列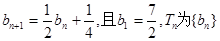 的前n项和。
的前n项和。
(1)求证:数列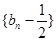 是等比数列,并求
是等比数列,并求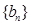 的通项公式;
的通项公式;
(2)如果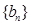 对任意
对任意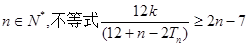 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
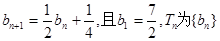 的前n项和。
的前n项和。(1)求证:数列
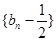 是等比数列,并求
是等比数列,并求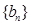 的通项公式;
的通项公式;(2)如果
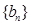 对任意
对任意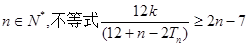 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。解: (1) 对任意
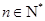 ,都有
,都有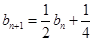 ,所以
,所以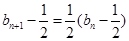 ……1分
……1分则
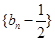 成等比数列,首项为
成等比数列,首项为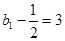 ,公比为
,公比为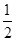 …………2分
…………2分所以
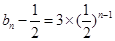 ,
, …………4分
…………4分(2) 因为

所以
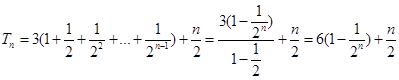 …………6分
…………6分因为不等式
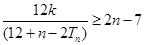 ,化简得
,化简得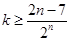 对任意
对任意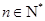 恒成立……7分
恒成立……7分设
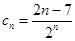 ,则
,则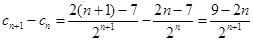 …………9分
…………9分当
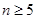 ,
,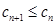 ,
,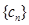 为单调递减数列,当
为单调递减数列,当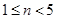 ,
,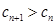 ,
,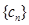 为单调递增数列
为单调递增数列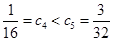 ,所以,
,所以, 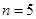 时,
时, 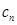 取得最大值
取得最大值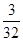 …………11分
…………11分所以, 要使
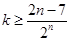 对任意
对任意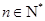 恒成立,
恒成立,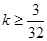
本试题主要是考查了等比数列的定义的运用,以及运用递推关系求解数列通项公式的运用,并且能借助于数列的和,放缩求证不等式的综合试题。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
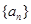 是一个等差数列,且
是一个等差数列,且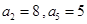 .等比数列
.等比数列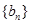 的前
的前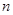 项和为
项和为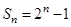 .
.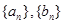 的通项公式;
的通项公式;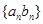 的最大项及相应
的最大项及相应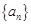 为等差数列,从
为等差数列,从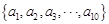 中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。
中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 个。 第10项开始比1大,则此等差数列的公差d的范围是( )
第10项开始比1大,则此等差数列的公差d的范围是( )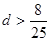
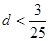

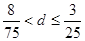
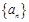 满足条件:
满足条件: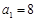 ,
,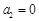 ,
,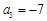 ,且数列
,且数列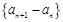
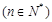 是等差数列.
是等差数列.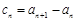 ,求数列
,求数列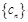 的通项公式;
的通项公式;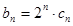 , 求
, 求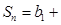
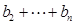 ;
;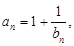 记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明:
记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明: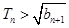
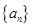 为等差数列,
为等差数列,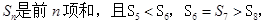 则下列结论错误的是( )
则下列结论错误的是( ) 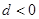
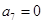
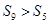
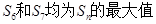
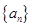 的前n项和为
的前n项和为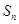 ,若
,若 则
则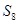 = ;
= ;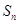 是等差数列
是等差数列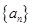 的前
的前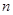 项和,且
项和,且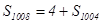 ,则
,则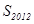 的值为( )
的值为( )