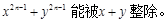题目内容
已知数列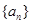 中,
中,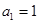 ,
,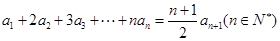
(Ⅰ)求数列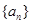 的通项公式;
的通项公式;
(Ⅱ)求数列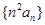 的前
的前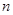 项和
项和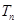 ;
;
(Ⅲ)(理科)若存在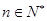 ,使得
,使得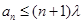 成立,求实数
成立,求实数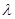 的最小值。
的最小值。
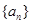 中,
中,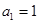 ,
,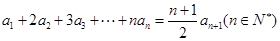
(Ⅰ)求数列
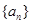 的通项公式;
的通项公式;(Ⅱ)求数列
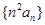 的前
的前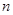 项和
项和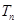 ;
;(Ⅲ)(理科)若存在
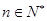 ,使得
,使得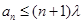 成立,求实数
成立,求实数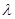 的最小值。
的最小值。(Ⅰ)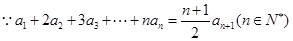 ┄┄┄ ①
┄┄┄ ①
 ┄┄┄ ②
┄┄┄ ②
由①-②得: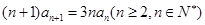
所以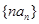 是从第二项起首项为2,公比为3的等比数列,则:
是从第二项起首项为2,公比为3的等比数列,则:
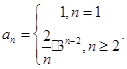
(Ⅱ)由(Ⅰ)可知当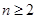 时,
时,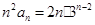
ⅰ当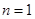 时,
时,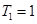
ⅱ当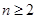 时,
时,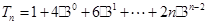 ┄┄┄ ③
┄┄┄ ③
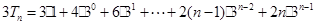 ┄┄┄ ④
┄┄┄ ④
由③-④得: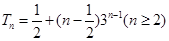
又当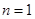 时,
时,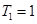 满足上式
满足上式
所以: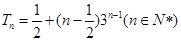
(Ⅲ)由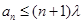 等价于
等价于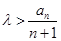 ,由(Ⅰ)可知,当
,由(Ⅰ)可知,当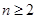 时,
时,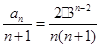
设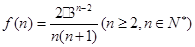 ,则
,则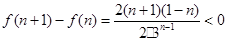
所以,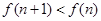 ,即
,即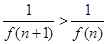
所以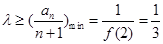 ,又因为
,又因为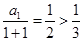
所以, 实数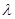 的最小值为
的最小值为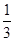 。
。
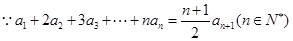 ┄┄┄ ①
┄┄┄ ① ┄┄┄ ②
┄┄┄ ②由①-②得:
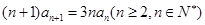
所以
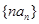 是从第二项起首项为2,公比为3的等比数列,则:
是从第二项起首项为2,公比为3的等比数列,则: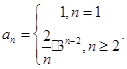
(Ⅱ)由(Ⅰ)可知当
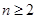 时,
时,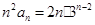
ⅰ当
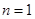 时,
时,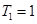
ⅱ当
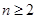 时,
时,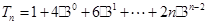 ┄┄┄ ③
┄┄┄ ③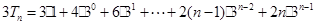 ┄┄┄ ④
┄┄┄ ④由③-④得:
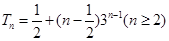
又当
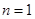 时,
时,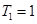 满足上式
满足上式所以:
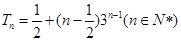
(Ⅲ)由
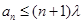 等价于
等价于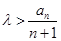 ,由(Ⅰ)可知,当
,由(Ⅰ)可知,当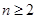 时,
时,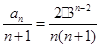
设
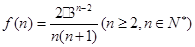 ,则
,则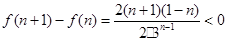
所以,
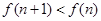 ,即
,即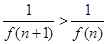
所以
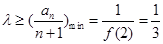 ,又因为
,又因为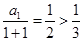
所以, 实数
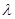 的最小值为
的最小值为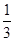 。
。略

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 第10项开始比1大,则此等差数列的公差d的范围是( )
第10项开始比1大,则此等差数列的公差d的范围是( )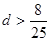
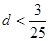

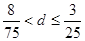
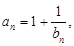 记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明:
记Tn是数列{an}的前n项之积,即Tn= b1·b 2·b 3…bn,试证明: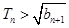
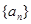 的前n项的和
的前n项的和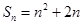 ,数列
,数列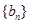 是正项等比数列,且满足
是正项等比数列,且满足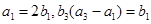 .
.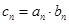 ,求数列
,求数列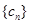 的前n项的和.
的前n项的和.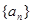 和
和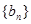 ,其前
,其前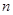 项和分别为
项和分别为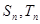 ,且
,且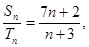 则
则 等于 ( )
等于 ( )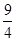
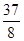
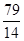
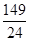
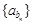 的前10项的和等于
的前10项的和等于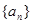 中,
中,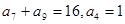 ,则
,则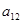 的值是( )
的值是( )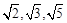 不可能成等差数列
不可能成等差数列