题目内容
【题目】在直角坐标系xOy中,点P(0, ![]() ),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .直线l的参数方程为
.直线l的参数方程为 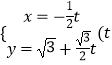 为参数).
为参数).
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() +
+ ![]() 的值.
的值.
【答案】解:(Ⅰ)∵曲线C的极坐标方程为 ![]() , ∴曲线C的直角坐标方程为
, ∴曲线C的直角坐标方程为 ![]() ,
,
∵直线l的参数方程为  为参数),
为参数),
∴消去t得直线l的普通方程为 ![]() .
.
(Ⅱ)点P(0, ![]() )在直线l:
)在直线l: ![]() 上,将直线l的参数方程代入曲线C的直角坐标方程,
上,将直线l的参数方程代入曲线C的直角坐标方程,
得2(﹣ ![]() )2+(
)2+( ![]() )2=4,∴5t2+12t﹣4=0,
)2=4,∴5t2+12t﹣4=0,
设两根为t1 , t2 , 则 ![]() ,
, ![]() ,故t1与t2异号,
,故t1与t2异号,
∴|PA|+|PB|=|t1﹣t2|= ![]() =
= ![]() ,
,
|PA||PB|=|t1t2|=﹣t1t2= ![]() ,
,
∴ ![]() +
+ ![]() =
= 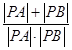 =
= ![]()
【解析】(Ⅰ)由曲线C的极坐标方程能求出曲线C的直角坐标方程;直线l的参数方程消去t,能求出直线l的普通方程.(Ⅱ)点P(0, ![]() )在直线l:
)在直线l: ![]() 上,将直线l的参数方程代入曲线C的直角坐标方程,得5t2+12t﹣4=0,设两根为t1 , t2 , 则
上,将直线l的参数方程代入曲线C的直角坐标方程,得5t2+12t﹣4=0,设两根为t1 , t2 , 则 ![]() ,
, ![]() ,由此能求出
,由此能求出 ![]() +
+ ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目