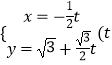题目内容

【题目】已知在平面直角坐标系 中的一个椭圆，它的中心在原点，左焦点为 ,右顶点为 ,设点 ．
（1）求该椭圆的标准方程；
（2）若 是椭圆上的动点，求线段 中点 的轨迹方程；

【答案】
（1）解：由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1．
又椭圆的焦点在x轴上, ∴椭圆的标准方程为
（2）解：设线段PA的中点为M（x,y）,点P的坐标是（x0,y0）,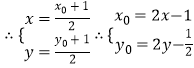

由点P在椭圆上,得 ,
∴线段PA中点M的轨迹方程是
【解析】（1）由椭圆的性质可得c,a的值，确定椭圆焦点在x轴，代入标准方程，即可解得。
（2）先判断A点的位置，再设P和M的坐标，将M的坐标用A和P的坐标表示出来，再代入椭圆的方程。
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．

练习册系列答案
相关题目

【题目】为了及时向群众宣传“十九大”党和国家“乡村振兴”战略，需要寻找一个宣讲站，让群众能在最短的时间内到宣讲站．设有三个乡镇，分别位于一个矩形的两个顶点及的中点处，，，现要在该矩形的区域内（含边界），且与等距离的一点处设一个宣讲站，记点到三个乡镇的距离之和为．

（Ⅰ）设，将表示为的函数；

（Ⅱ）试利用（Ⅰ）的函数关系式确定宣讲站的位置，使宣讲站到三个乡镇的距离之和最小．

【题目】在直角坐标系xOy中，点P（0， ），以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为 ．直线l的参数方程为 为参数）．
（Ⅰ）写出曲线C的直角坐标方程和直线l的普通方程；
（Ⅱ）设直线l与曲线C的两个交点分别为A，B，求 + 的值．

【题目】已知双曲线 ﹣ =1（a＞0，b＞0）的实轴端点分别为A1 ， A2 ， 记双曲线的其中的一个焦点为F，一个虚轴端点为B，若在线段BF上（不含端点）有且仅有两个不同的点Pi（i=1，2），使得∠A1PiA2= ，则双曲线的离心率e的取值范围是（ ）
A.（ ， ）
B.（ ， ）
C.（1， ）
D.（ ，+∞）

【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且 ．
（1）求sinB的值；
（2）若D为AC的中点，且BD=1，求△ABD面积的最大值．

【题目】已知抛物线的对称轴为坐标轴，顶点是坐标原点，准线方程为 ，直线 与抛物线相交于不同的 ， 两点．
（1）求抛物线的标准方程；
（2）如果直线 过抛物线的焦点，求 的值；
（3）如果 ，直线 是否过一定点，若过一定点，求出该定点；若不过一定点，试说明理由．

【题目】已知命题 ，命题 ，若 是 的必要不充分条件，则实数 的取值范围是 .

【题目】某企业准备投资 万元兴办一所中学，对当地教育市场进行调查后，得到了如下的数据表格（以班级为单位）：

初中

26

4

高中

54

6

第一年因生源和环境等因素，全校总班级至少 个，至多 个，若每开设一个初、高中班，可分别获得年利润 万元、 万元，则第一年利润最大为

A. 万元 B. 万元 C. 万元 D. 万元

【题目】某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组： ，并整理得到如下频率分布直方图：

（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网