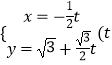题目内容
【题目】已知在四棱锥C﹣ABDE中,DB⊥平面ABC,AE∥DB,△ABC是边长为2的等边三角形,AE=1,M为AB的中点. 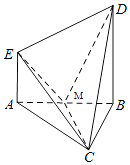
(1)求证:CM⊥EM;
(2)若直线DM与平面ABC所成角的正切值为2,求二面角B﹣CD﹣E的大小.
【答案】
(1)证明:∵△ABC是等边三角形,M为AB的中点,∴CM⊥AB.
又∵DB⊥平面ABC,
∴DB⊥CM,∴CM⊥平面ABDE,
∵EM平面ABDE,∴CM⊥EM
(2)解:如图,以点M为坐标原点,MC,MB所在直线分别为x,y轴,
过M且与直线BD平行的直线为z轴,建立空间直角坐标系.
∵DB⊥平面ABC,∴∠DMB为直线DM与平面ABC所成的角.
由题意得tan ![]() ,即BD=2,故B(0,1,0),C(
,即BD=2,故B(0,1,0),C( ![]() ),D(0,1,2),E(0,﹣1,1),
),D(0,1,2),E(0,﹣1,1),
∴ ![]() =(
=( ![]() ),
), ![]() =(0,0,2),
=(0,0,2), ![]() =(﹣
=(﹣ ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
),
设平面BCD与平面CDE的法向量分别为 ![]() =(x,y,z),
=(x,y,z), ![]() =(a,b,c),
=(a,b,c),
则  ,令x=1,得
,令x=1,得 ![]() =(1,
=(1, ![]() ,0).
,0).
同理求得 ![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() ),
),
∴cos< ![]() >=
>=  =0,∴二面角B﹣CD﹣E的大小为90°.
=0,∴二面角B﹣CD﹣E的大小为90°.

【解析】(1)推导出CM⊥AB,DB⊥CM,从而CM⊥平面ABDE,由此能证明CM⊥EM.(2)以点M为坐标原点,MC,MB所在直线分别为x,y轴,过M且与直线BD平行的直线为z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣CD﹣E的大小.
【考点精析】通过灵活运用直线与平面垂直的性质和空间角的异面直线所成的角,掌握垂直于同一个平面的两条直线平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.

【题目】某企业准备投资 ![]() 万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
|
| |
初中 | 26 | 4 |
高中 | 54 | 6 |
第一年因生源和环境等因素,全校总班级至少 ![]() 个,至多
个,至多 ![]() 个,若每开设一个初、高中班,可分别获得年利润
个,若每开设一个初、高中班,可分别获得年利润 ![]() 万元、
万元、 ![]() 万元,则第一年利润最大为
万元,则第一年利润最大为 ![]()
A. ![]() 万元 B.
万元 B. ![]() 万元 C.
万元 C. ![]() 万元 D.
万元 D. ![]() 万元
万元