题目内容
【题目】已知函数![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)若存在实数![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由绝对值定义将不等式化为三个不等式组,分别求解集,最后求并集(2)先化简不等式为|3x﹣a|﹣|3x+6|≥1﹣a,再根据绝对值三角不等式得|3x﹣a|﹣|3x+6|最大值为|a+6|,最后解不等式得实数![]() 的取值范围
的取值范围
试题解析:解:(1)a=2时:f(x)=|3x﹣2|﹣|x+2|≤3,
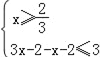 或
或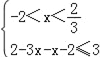 或
或![]() ,
,
解得:﹣![]() ≤x≤
≤x≤![]() ;
;
(2)不等式f(x)≥1﹣a+2|2+x|成立,
即|3x﹣a|﹣|3x+6|≥1﹣a,
由绝对值不等式的性质可得||3x﹣a|﹣|3x+6||≤|(3x﹣a)﹣(3x+6)|=|a+6|,
即有f(x)的最大值为|a+6|,
∴![]() 或
或![]() ,
,
解得:a≥﹣![]() .
.

练习册系列答案
相关题目
【题目】调查在![]() 级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
(1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为![]() 级风的海上航行中晕船与性别有关?
级风的海上航行中晕船与性别有关?
晕船 | 不晕船 | 总计 | |
男人 | |||
女人 | |||
总计 |
附:.![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |