题目内容
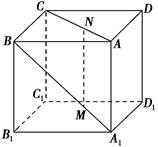
如图,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=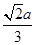 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).
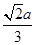 ,则MN与平面BB1C1C的位置关系是 ( ).
,则MN与平面BB1C1C的位置关系是 ( ).
| A.相交 | B.平行 | C.垂直 | D.不能确定 |
B
分别以C1B1,C1D1,C1C所在直线为x,y,z轴,建立空间直角坐标系,如图所示.
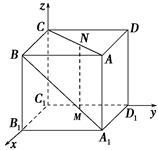
∵A1M=AN=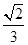 a,∴M
a,∴M ,N
,N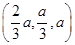 ,∴
,∴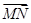 =
=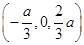 .
.
又C1(0,0,0),D1(0,a,0),∴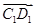 =(0,a,0),
=(0,a,0),
∴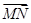 ·
·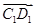 =0,∴
=0,∴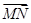 ⊥
⊥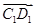 .
.
∵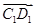 是平面BB1C1C的法向量,
是平面BB1C1C的法向量,
且MN?平面BB1C1C,∴MN∥平面BB1C1C.

∵A1M=AN=
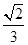 a,∴M
a,∴M ,N
,N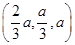 ,∴
,∴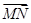 =
=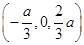 .
.又C1(0,0,0),D1(0,a,0),∴
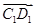 =(0,a,0),
=(0,a,0),∴
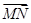 ·
·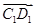 =0,∴
=0,∴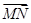 ⊥
⊥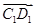 .
.∵
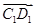 是平面BB1C1C的法向量,
是平面BB1C1C的法向量,且MN?平面BB1C1C,∴MN∥平面BB1C1C.

练习册系列答案
相关题目
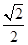 AB.
AB.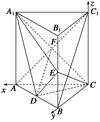
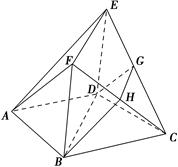
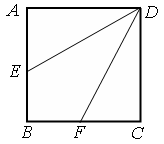
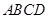 中,点
中,点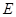 是
是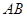 的中点,点
的中点,点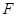 是
是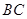 的中点,将△
的中点,将△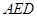 、△
、△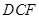 分别沿
分别沿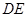 、
、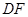 折起,使
折起,使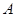 、
、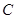 两点重合于点
两点重合于点 ,连接
,连接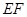 ,
,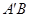 .
.
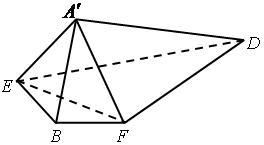
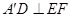 ;
;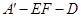 的余弦值.
的余弦值.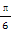

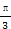

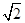 ,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.
,PA⊥PD,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O为AD中点.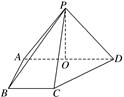
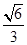 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.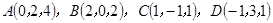 ,E,F分别是AB与CD的中点,则EF的长为( )
,E,F分别是AB与CD的中点,则EF的长为( )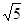
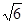
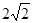
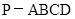 中,底面
中,底面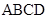 是菱形,
是菱形,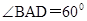 ,
,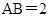 ,
,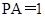 ,
,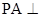 平面
平面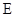 是
是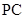 的中点,
的中点,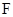 是
是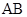 的中点.
的中点. 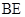 ∥平面
∥平面 ;
; ;
; 所成的锐二面角的大小.
所成的锐二面角的大小.