题目内容
【题目】已知数列{an}的前n项和为Sn ， 且满足 
，设{Sn}的前n项和为Tn ， T2017= ．
【答案】
【解析】解：由Sn=（﹣1）nan+ 
， 当n≥2时，an=Sn﹣Sn﹣1=（﹣1）nan﹣（﹣1）n﹣1an﹣1﹣ ．
n=2k（k∈N*）为偶数时，a2k﹣1= 
，
n=2k+1为奇数时，2a2k+1+a2k=﹣ 
，∴a2k=﹣ ．
∴﹣a2k﹣1+a2k=﹣ 
，
∴T2017=（﹣a1+a2﹣a3+…﹣a2015+a2016﹣a2017）+ 
=﹣2（ 
+…+ 
）+
=﹣2×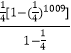 
+ 
= ．
所以答案是： ．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系
．
名校课堂系列答案
【题目】为调查高中生的数学成绩与学生自主学习时间之间的相关关系，某重点高中数学教师对新入学的45名学生进行了跟踪调查，其中每周自主做数学题的时间不少于15小时的有19人，余下的人中，在高三模拟考试中数学平均成绩不足120分的占 
，统计成绩后，得到如下的2×2列联表：
分数大于等于120分 | 分数不足120分 | 合 计 | |
周做题时间不少于15小时 |
| 4 | 19 |
周做题时间不足15小时 |
|
|
|
合 计 |
|
| 45 |
（Ⅰ）请完成上面的2×2列联表，并判断能否在犯错误的概率不超过0.01的前提下认为“高中生的数学成绩与学生自主学习时间有关”；
（Ⅱ）（i） 按照分层抽样的方法，在上述样本中，从分数大于等于120分和分数不足120分的两组学生中抽取9名学生，设抽到的不足120分且周做题时间不足15小时的人数是X，求X的分布列（概率用组合数算式表示）；
（ii） 若将频率视为概率，从全校大于等于120分的学生中随机抽取20人，求这些人中周做题时间不少于15小时的人数的期望和方差．
附： 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
