题目内容
用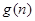 表示自然数
表示自然数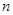 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9,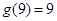 ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,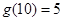 ,那么
,那么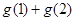
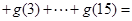 ;
;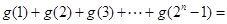 .
.
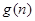 表示自然数
表示自然数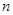 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9,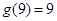 ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,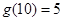 ,那么
,那么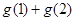
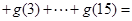 ;
;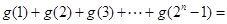 .
.85, (4n-1).
(4n-1).
 (4n-1).
(4n-1).此题答案为:85, (4n-1)
(4n-1)
据题中对g(n)的定义,判断出g(n)=g(2n),且若n为奇数则g(n)=n,利用等差数列的前n项和公式及逐差累加的方法及等比数列的前n项和公式求出g(1)+g(2)+g(3)+…+g(2n-1),令n=4求出g(1)+g(2)+g(3)+…+g(15).
解:由g(n)的定义易知g(n)=g(2n),且若n为奇数则g(n)=n
令f(n)=g(1)+g(2)+g(3)+…g(2n-1)
则f(n+1)=g(1)+g(2)+g(3)+…g(2n+1-1)=1+3+…+(2n+1-1)+g(2)+g(4)+…+g(2n+1-2)
=2n[1+(2n+1-1)]/2+g(1)+g(2)+…+g(2n+1-2)=4n+f(n)
即f(n+1)-f(n)=4n
分别取n为1,2,…,n并累加得f(n+1)-f(1)=4+42+…+4n=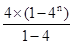 =
= (4n-1)
(4n-1)
又f(1)=g(1)=1,所以f(n+1)= (4n-1)+1
(4n-1)+1
所以f(n)=g(1)+g(2)+g(3)+…g(2n-1)= (4n-1-1)+1
(4n-1-1)+1
令n=4得
g(1)+g(2)+g(3)+…+g(15)= (43-1)+1=85
(43-1)+1=85
故答案为85, (4n-1).
(4n-1).
 (4n-1)
(4n-1)据题中对g(n)的定义,判断出g(n)=g(2n),且若n为奇数则g(n)=n,利用等差数列的前n项和公式及逐差累加的方法及等比数列的前n项和公式求出g(1)+g(2)+g(3)+…+g(2n-1),令n=4求出g(1)+g(2)+g(3)+…+g(15).
解:由g(n)的定义易知g(n)=g(2n),且若n为奇数则g(n)=n
令f(n)=g(1)+g(2)+g(3)+…g(2n-1)
则f(n+1)=g(1)+g(2)+g(3)+…g(2n+1-1)=1+3+…+(2n+1-1)+g(2)+g(4)+…+g(2n+1-2)
=2n[1+(2n+1-1)]/2+g(1)+g(2)+…+g(2n+1-2)=4n+f(n)
即f(n+1)-f(n)=4n
分别取n为1,2,…,n并累加得f(n+1)-f(1)=4+42+…+4n=
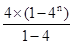 =
= (4n-1)
(4n-1)又f(1)=g(1)=1,所以f(n+1)=
 (4n-1)+1
(4n-1)+1所以f(n)=g(1)+g(2)+g(3)+…g(2n-1)=
 (4n-1-1)+1
(4n-1-1)+1令n=4得
g(1)+g(2)+g(3)+…+g(15)=
 (43-1)+1=85
(43-1)+1=85故答案为85,
 (4n-1).
(4n-1).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
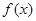 是定义在R上的且以2为周期的偶函数,当
是定义在R上的且以2为周期的偶函数,当 时,
时, ,如果直线
,如果直线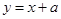 与曲线
与曲线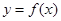 恰有两个不同的交点,则实数
恰有两个不同的交点,则实数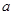 的值为 ( )
的值为 ( )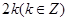
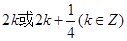
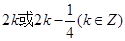
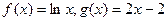 .
.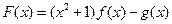 在
在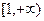 上的单调性;
上的单调性;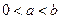 时,求证:函数
时,求证:函数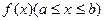 的值域的长度大于
的值域的长度大于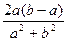 (闭区间[m,n]的长度定义为n-m).
(闭区间[m,n]的长度定义为n-m).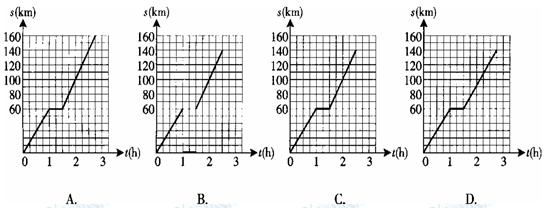
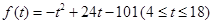 ,
,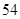 B.
B.
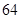 D.
D.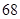
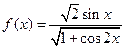 ,
, 的定义域、值域、最小正周期;
的定义域、值域、最小正周期;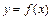 是定义在区间
是定义在区间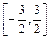 上的偶函数,且
上的偶函数,且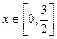 时,
时,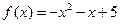 (1).求函数
(1).求函数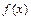 的解析式;(2).若矩形
的解析式;(2).若矩形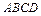 的顶点
的顶点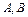 在函数
在函数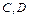 在
在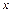 轴上,求矩形
轴上,求矩形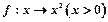 是集合A到集合B的映射,如果B=
是集合A到集合B的映射,如果B=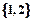 ,则
,则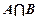 = .
= .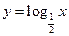 与函数
与函数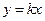 的图象有公共点
的图象有公共点 ,且点
,且点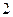 ,
,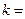 __________.
__________.