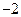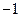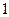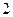题目内容
已知函数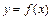 是定义在区间
是定义在区间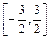 上的偶函数,且
上的偶函数,且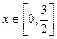 时,
时,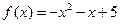 (1).求函数
(1).求函数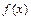 的解析式;(2).若矩形
的解析式;(2).若矩形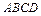 的顶点
的顶点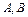 在函数
在函数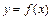 的图像上,顶点
的图像上,顶点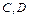 在
在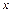 轴上,求矩形
轴上,求矩形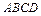 的面积的最大值。
的面积的最大值。
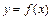 是定义在区间
是定义在区间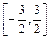 上的偶函数,且
上的偶函数,且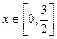 时,
时,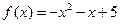 (1).求函数
(1).求函数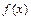 的解析式;(2).若矩形
的解析式;(2).若矩形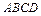 的顶点
的顶点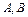 在函数
在函数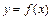 的图像上,顶点
的图像上,顶点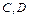 在
在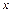 轴上,求矩形
轴上,求矩形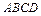 的面积的最大值。
的面积的最大值。(1)f(x)= ;(2)当t=1时,矩形ABCD的面积取得最大值6.
;(2)当t=1时,矩形ABCD的面积取得最大值6.
 ;(2)当t=1时,矩形ABCD的面积取得最大值6.
;(2)当t=1时,矩形ABCD的面积取得最大值6.(1)当 所以f(-x)=-(-x)2-(-x)+5=-x2+x+5,
所以f(-x)=-(-x)2-(-x)+5=-x2+x+5,
又因为f(x)是偶函数,所以f(x)=f(-x)=-x2+x+5,
所以f(x)=
(2)由题意,不妨设A点在第一象限,坐标为(t,-t2-t+5)其中,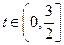 ,
,
则S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t. ,
,
令 得
得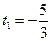 (舍去),t2=1.
(舍去),t2=1.
当 时
时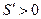 ,所以S(t)在
,所以S(t)在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
所以当t=1时,ABCD的面积取得极大值也是S(t)在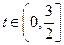 上的最大值。
上的最大值。
从而当t=1时,矩形ABCD的面积取得最大值6.
 所以f(-x)=-(-x)2-(-x)+5=-x2+x+5,
所以f(-x)=-(-x)2-(-x)+5=-x2+x+5,又因为f(x)是偶函数,所以f(x)=f(-x)=-x2+x+5,
所以f(x)=

(2)由题意,不妨设A点在第一象限,坐标为(t,-t2-t+5)其中,
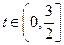 ,
,则S(t)=S ABCD=2t(-t2-t+5)=-2t3-2t2+10t.
 ,
,令
 得
得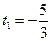 (舍去),t2=1.
(舍去),t2=1.当
 时
时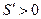 ,所以S(t)在
,所以S(t)在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,所以当t=1时,ABCD的面积取得极大值也是S(t)在
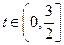 上的最大值。
上的最大值。从而当t=1时,矩形ABCD的面积取得最大值6.

练习册系列答案
相关题目
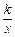 +
+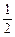 x2在 (0,
x2在 (0,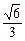 ]上是单调减函数,求实数k的取值范围;
]上是单调减函数,求实数k的取值范围;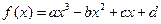 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值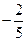 .
.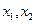 ∈[-1,1],不等式
∈[-1,1],不等式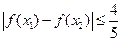 成立;
成立;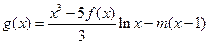 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.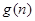 表示自然数
表示自然数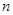 的所有因数中最大的那个奇数,例如:9的因数有1,3,9,
的所有因数中最大的那个奇数,例如:9的因数有1,3,9,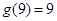 ,10的因数有1,2,5,10,
,10的因数有1,2,5,10,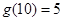 ,那么
,那么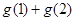
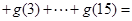 ;
;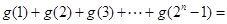 .
.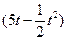 万元
万元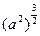 =a3 ②
=a3 ②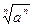 =|a| ③函数y=
=|a| ③函数y=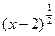 -(3x-7)0的定义域是(2, +∞) ④若
-(3x-7)0的定义域是(2, +∞) ④若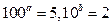 ,则2a+b=1
,则2a+b=1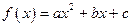 .
. 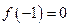 ,试判断函数
,试判断函数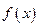 零点个数;
零点个数;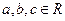 ,使
,使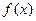 同时满足以下条件①对
同时满足以下条件①对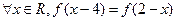 ,且
,且 ;②对
;②对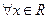 ,都有
,都有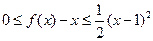 。若存在,求出
。若存在,求出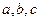 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。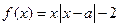 .
.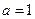 时,解不等式
时,解不等式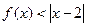 ;
; 时,
时,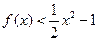 恒成立,求实数
恒成立,求实数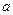 的取值范围.
的取值范围.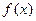 是
是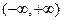 上的偶函数,若对于
上的偶函数,若对于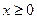 ,都有
,都有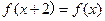 ,且当
,且当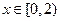 时,
时,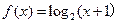 ,则
,则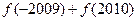 的值为 ( )
的值为 ( )