جâؤ؟ؤعبف
،¾جâؤ؟،؟زٍ؟حء÷ء؟ءظت±شِ´َ£¬ؤ³ذ¬µêؤâسأز»¸ِ¸كخھ50![]() £¨¼´
£¨¼´![]() £©µؤئ½أو¾µ×شضئز»¸ِتْض±°ع·إµؤ¼ٍز×ذ¬¾µ£¬¸ù¾ف¾رé£؛ز»°م¹ث؟ح
£©µؤئ½أو¾µ×شضئز»¸ِتْض±°ع·إµؤ¼ٍز×ذ¬¾µ£¬¸ù¾ف¾رé£؛ز»°م¹ث؟ح![]() µؤرغ¾¦
µؤرغ¾¦![]() µ½µطأوµؤ¾àہëخھ
µ½µطأوµؤ¾àہëخھ![]() £¨
£¨![]() £©شعاّ¼ن
£©شعاّ¼ن![]() ؤع£¬ةèض§¼ـ
ؤع£¬ةèض§¼ـ![]() ¸كخھ
¸كخھ![]() £¨
£¨![]() £©
£©![]() £¬
£¬![]() £¬¹ث؟ح؟ةتسµؤ¾µدٌ·¶خ§خھ
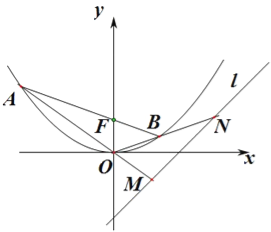
£¬¹ث؟ح؟ةتسµؤ¾µدٌ·¶خ§خھ![]() £¨بçح¼ثùت¾£©£¬¼ا
£¨بçح¼ثùت¾£©£¬¼ا![]() µؤ³¤¶بخھ
µؤ³¤¶بخھ![]() £¨
£¨![]() £©.
£©.
£¨I£©µ±![]() ت±£¬تشاَ
ت±£¬تشاَ![]() ¹طسع
¹طسع![]() µؤ؛¯ت¹طدµت½؛ح
µؤ؛¯ت¹طدµت½؛ح![]() µؤ×î´َضµ£»
µؤ×î´َضµ£»
£¨II£©µ±¹ث؟حµؤذ¬![]() شع¾µضذµؤدٌ
شع¾µضذµؤدٌ![]() آْ×م²»µب¹طدµ
آْ×م²»µب¹طدµ![]() £¨²»¼ئذ¬³¤£©ت±£¬³ئ¹ث؟ح؟ةشع¾µضذ؟´µ½×ش¼؛µؤذ¬£¬بôت¹ز»°م¹ث؟ح¶¼ؤـشع¾µضذ؟´µ½×ش¼؛µؤذ¬£¬تشاَ
£¨²»¼ئذ¬³¤£©ت±£¬³ئ¹ث؟ح؟ةشع¾µضذ؟´µ½×ش¼؛µؤذ¬£¬بôت¹ز»°م¹ث؟ح¶¼ؤـشع¾µضذ؟´µ½×ش¼؛µؤذ¬£¬تشاَ![]() µؤب،ضµ·¶خ§.
µؤب،ضµ·¶خ§.
،¾´ً°¸،؟£¨I£©¼û½âخِ£»£¨II£©![]() .
.
،¾½âخِ،؟
£¨I£©¸ù¾فب½اذخµؤدàثئ£¬اَ³ِ![]() £¬
£¬![]() µؤ³¤£¬´س¶ّ؟ة¹¹½¨؛¯ت£¬اَµ¼ت£¬ب·¶¨؛¯تµؤµ¥µ÷ذش£¬¼´؟ةاَµأ½لآغ£»£¨II£©¸ù¾فب½اذخµؤدàثئ£¬اَ³ِ
µؤ³¤£¬´س¶ّ؟ة¹¹½¨؛¯ت£¬اَµ¼ت£¬ب·¶¨؛¯تµؤµ¥µ÷ذش£¬¼´؟ةاَµأ½لآغ£»£¨II£©¸ù¾فب½اذخµؤدàثئ£¬اَ³ِ![]() £¬
£¬![]() £¬سةجâزâضھ
£¬سةجâزâضھ![]() £¬¼´
£¬¼´![]() ¶ش
¶ش![]() ؛م³ةء¢£¬´س¶ّ
؛م³ةء¢£¬´س¶ّ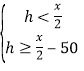 ¶ش
¶ش![]() ؛م³ةء¢£¬سة´ث؟ةاَµأ
؛م³ةء¢£¬سة´ث؟ةاَµأ![]() µؤب،ضµ·¶خ§.
µؤب،ضµ·¶خ§.
£¨I£©زٍخھ![]() £¬
£¬![]() £¬ثùزشسة
£¬ثùزشسة![]() £¬¼´
£¬¼´![]() £¬½âµأ
£¬½âµأ![]() £¬ح¬ہي£¬سة
£¬ح¬ہي£¬سة![]() £¬¼´
£¬¼´![]() £¬½âµأ
£¬½âµأ![]() £¬ثùزش
£¬ثùزش![]() £¬
£¬![]() زٍخھ
زٍخھ![]() £¬ثùزش
£¬ثùزش![]() شع
شع![]() ةدµ¥µ÷µف¼ُ£¬¹تµ±
ةدµ¥µ÷µف¼ُ£¬¹تµ±![]() ت±£¬
ت±£¬![]() ب،µأ×î´َضµخھ
ب،µأ×î´َضµخھ![]()
£¨II£©سة![]() £¬µأ
£¬µأ![]() £¬سة
£¬سة![]() £¬µأ
£¬µأ![]() £¬ثùزشسةجâزâضھ
£¬ثùزشسةجâزâضھ![]() £¬¼´
£¬¼´![]() ¶ش
¶ش![]() ؛م³ةء¢£¬´س¶ّ
؛م³ةء¢£¬´س¶ّ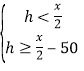 ¶ش
¶ش![]() ؛م³ةء¢£¬½âµأ
؛م³ةء¢£¬½âµأ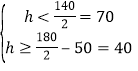 £¬¹ت
£¬¹ت![]() µؤب،ضµ·¶خ§تا
µؤب،ضµ·¶خ§تا![]()

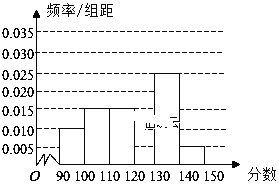
،¾جâؤ؟،؟ؤ³ر§ذ£خھµ÷²é¸كبؤ꼶ر§ةْµؤةي¸كاé؟ِ£¬°´ثو»ْ³éرùµؤ·½·¨³éب،80أûر§ةْ£¬µأµ½ؤذةْةي¸كاé؟ِµؤئµآت·ض²¼ض±·½ح¼£¨ح¼1£©؛حإ®ةْةي¸كاé؟ِµؤئµآت·ض²¼ض±·½ح¼£¨ح¼2£©.زرضھح¼1ضذةي¸كشع170،«175cmµؤؤذةْبثتسذ16بث
.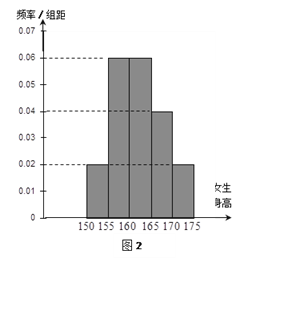

(1)¸ù¾فئµآت·ض²¼ض±·½ح¼£¬حê³ةدآءذµؤ![]() ءذءھ±ي£¬²¢إذ¶دؤـسذ¶à´َ£¨°ظ·ض±ب£©µؤ°رخصبدخھ،°ةي¸كسëذش±ًسذ¹ط،±£؟
ءذءھ±ي£¬²¢إذ¶دؤـسذ¶à´َ£¨°ظ·ض±ب£©µؤ°رخصبدخھ،°ةي¸كسëذش±ًسذ¹ط،±£؟
|
| ×ـ¼ئ | |
ؤذةْةي¸ك | |||
إ®ةْةي¸ك | |||
×ـ¼ئ |
(2)شعةدتِ80أûر§ةْضذ£¬´سةي¸كشع170-175cmض®¼نµؤر§ةْ°´ؤذ،¢إ®ذش±ً·ض²م³éرùµؤ·½·¨£¬³é³ِ5بث£¬´سصâ5بثضذر،إة3بثµ±ئىتض£¬اَ3بثضذا،؛أسذز»أûإ®ةْµؤ¸إآت.
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
²خ؟¼¹«ت½¼°²خ؟¼ت¾فبçدآ£؛
![]()