题目内容
【题目】在给出的下列命题中,正确的是( )
A.设![]() 是同一平面上的四个点,若
是同一平面上的四个点,若![]() ,则点
,则点![]() 必共线
必共线
B.若向量![]() 是平面
是平面![]() 上的两个向量,则平面
上的两个向量,则平面![]() 上的任一向量
上的任一向量![]() 都可以表示为
都可以表示为![]() ,且表示方法是唯一的
,且表示方法是唯一的
C.已知平面向量![]() 满足
满足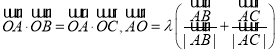 则
则![]() 为等腰三角形
为等腰三角形
D.已知平面向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 是等边三角形
是等边三角形
【答案】ACD
【解析】
对于A,根据共线定理判断A、B、C三点共线即可;对于B,根据平面向量的基本定理,判断命题错误;对于C,根据向量的运算性质可得OA为BC的垂线且OA在![]() 的角平分线上,从而可判断C;对于D,根据平面向量的线性表示与数量积运算得出命题正确;
的角平分线上,从而可判断C;对于D,根据平面向量的线性表示与数量积运算得出命题正确;
对于A,![]() ,
,
∴![]() ,∴
,∴![]() ,且有公共点C,
,且有公共点C,
∴则点A、B、C共线,命题A正确;
对于B,根据平面向量的基本定理缺少条件![]() 不共线,故B错误;
不共线,故B错误;
对于C,由于![]() ,即
,即![]() ,
,![]() ,
,
得![]() ,即OA为BC的垂线,
,即OA为BC的垂线,
又由于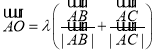 ,可得OA在
,可得OA在![]() 的角平分线上,
的角平分线上,
综合得![]() 为等腰三角形,故C正确;
为等腰三角形,故C正确;
对于D,平面向量![]() 、
、![]() 、
、![]() 满足
满足![]() ,且
,且![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即![]() ,∴
,∴![]() ,
,
∴![]() 、
、![]() 的夹角为
的夹角为![]() ,同理
,同理![]() 、
、![]() 的夹角也为
的夹角也为![]() ,
,
∴![]() 是等边三角形,故D正确;
是等边三角形,故D正确;
故选ACD.

练习册系列答案
相关题目
【题目】某超市计划销售某种食品,现邀甲、乙两个商家进场试销5天.两个商家提供的返利方案如下:甲商家每天固定返利60元,且每卖出一件食品商家再返利2元;乙商家无固定返利,卖出30件以内(含30件)的食品,每件食品商家返利4元,超出30件的部分每件返利6元.经统计,两个商家的试销情况茎叶图如下:
甲 | 乙 | |||||||
9 | 8 | 9 | 2 | 8 | 8 | |||
2 | 2 | 3 | 2 | 1 | 1 | |||
(1)现从甲商家试销的5天中抽取两天,求这两天的销售量都小于30的概率;
(2)超市拟在甲、乙两个商家中选择一家长期销售,如果仅从日平均返利额的角度考虑,请利用所学的统计学知识为超市作出选择,并说明理由.