题目内容
18.设f(x)和g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在[a,b]上有2个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=-x2+(m+2)x-1和g(x)=2x+3是[1,5]上的“关联函数”,则实数m的取值范围为(4,5].分析 由题意可得y=h(x)=f(x)-g(x)=-x2+mx-4在[1,5]上有两个不同的零点,有$\left\{\begin{array}{l}f(1)≤0\\ f(5)≤0\\ f(\frac{m}{2})>0\\ 1<\frac{m}{2}<5\end{array}\right.$,由此求得m的取值范围
解答 解:∵f(x)=-x2+(m+2)x-1和g(x)=2x+3在[1,5]上是“关联函数”,
故函数y=h(x)=f(x)-g(x)=-x2+mx-4在[1,5]上有两个不同的零点,
有$\left\{\begin{array}{l}f(1)≤0\\ f(5)≤0\\ f(\frac{m}{2})>0\\ 1<\frac{m}{2}<5\end{array}\right.$,即$\left\{\begin{array}{l}m-5≤0\\ 5m-29≤0\\ \frac{{m}^{2}}{4}-4>0\\ 2<m<10\end{array}\right.$,
解得m∈(4,5],
故答案为:(4,5]
点评 本题考查函数零点的判定定理,“关联函数”的定义,二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.某连锁经营公司的5个零售店某月的销售额和利润额资料如表:
(1)若销售额和利润额具有线性相关关系,用最小乘法计算利润额y对销售额x的回归直线方程;
(2)若商店F此月的销售额为1亿1千万元,试用(1)中求得的回归方程,估测其利润.(精确到百万元)
| 商店名称 | A | B | C | D | E |
| 销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
| 利润(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(2)若商店F此月的销售额为1亿1千万元,试用(1)中求得的回归方程,估测其利润.(精确到百万元)
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},0≤x<a}\\{{2}^{x},x≥a}\end{array}\right.$,若存在实数b,使函数g(x)=f(x)-b有两个零点,则实数a的取值范围是( )
| A. | (0,2) | B. | (2,+∞) | C. | (2,4) | D. | (4,+∞) |
7.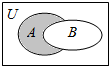 集合U=R,A={x|x2-x-2<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合是( )
集合U=R,A={x|x2-x-2<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合是( )
 集合U=R,A={x|x2-x-2<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合是( )
集合U=R,A={x|x2-x-2<0},B={x|y=ln(1-x)},则图中阴影部分表示的集合是( )| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x≤1} |
8.有下列说法其正确是( )
| A. | 0与{0}表示同一个集合 | |
| B. | 由1,2,3组成的集合可表示为{1,2,3}或{3,2,1} | |
| C. | 方程(x-1)2(x-2)=0的所有解的集合可表示为{1,1,2} | |
| D. | 集合{x|4<x<5}是有限集 |
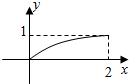 已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].
已知函数y=f(x)是定义在区间[-2,2]上的奇函数,当0≤x≤2时的图象如图所示,则y=f(x)的值域为[-1,1].