题目内容
9.求由抛物线y=x2-2x+5与直线y=x+5所围成的图形的面积S.分析 由抛物线y=x2-2x+5与直线y=x+5得x2-3x=0,解得:x=0,或x=3,依题意,由抛物线y=x2-2x+5与直线y=x+5所围成的图形的面积S=${∫}_{0}^{3}$[(x+5)-(x2-2x+5)]dx,利用微积分定理可得答案.
解答 解:由抛物线y=x2-2x+5与直线y=x+5得x2-3x=0,解得:x=0,或x=3,
故积分区间[0,3],
由抛物线y=x2-2x+5与直线y=x+5所围成的图形的面积S=${∫}_{0}^{3}$[(x+5)-(x2-2x+5)]dx
=($\frac{3}{2}$x2-$\frac{1}{3}$x3)${|}_{0}^{3}$=$\frac{3}{2}×9-\frac{1}{3}×27$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查定积分在求面积中的应用,得到由抛物线y=x2-2x+5与直线y=x+5所围成的图形的面积S=${∫}_{0}^{3}$[(x+5)-(x2-2x+5)]dx是关键,考查等价转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目

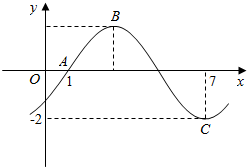 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.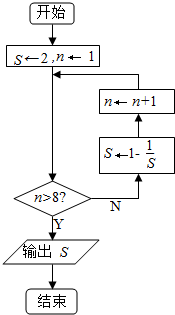 执行如图所示的算法流程图,则输出的结果是-1.
执行如图所示的算法流程图,则输出的结果是-1.