题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},0≤x<a}\\{{2}^{x},x≥a}\end{array}\right.$,若存在实数b,使函数g(x)=f(x)-b有两个零点,则实数a的取值范围是( )| A. | (0,2) | B. | (2,+∞) | C. | (2,4) | D. | (4,+∞) |
分析 由g(x)=f(x)-b有两个零点可得f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a的范围.
解答  解:∵g(x)=f(x)-b有两个零点
解:∵g(x)=f(x)-b有两个零点
∴f(x)=b有两个零点,即y=f(x)与y=b的图象有两个交点,
由于y=x2在[0,a)递增,y=2x在[a,+∞)递增,
要使函数f(x)在[0,+∞)不单调,
即有a2>2a,由g(a)=a2-2a,g(2)=g(4)=0,
可得2<a<4.
故选C.
点评 本题考查函数的零点问题,渗透了转化思想,数形结合的数学思想,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
5.已知数列{an}中,a1=1,且满足an+1=an+2n,n∈N+,则a10=( )
| A. | 19 | B. | 91 | C. | 101 | D. | 121 |
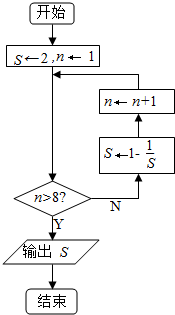 执行如图所示的算法流程图,则输出的结果是-1.
执行如图所示的算法流程图,则输出的结果是-1.