题目内容
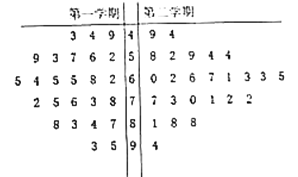
【题目】为评估![]() 设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
设备生产某种零件的性能,从该设备生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 78 | 79 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 93 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的频率):
表示相应事件的频率):
①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.试判断![]() 设备的性能等级.
设备的性能等级.
(2)将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“次品”,将直径小于等于
的零件认定为是“次品”,将直径小于等于![]() 的零件或直径大于等于
的零件或直径大于等于![]() 的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数
的零件认定为是“突变品”,从样本的“次品”中随意抽取2件零件,求“突变品”个数![]() 的数学期望.
的数学期望.
【答案】(1)丙;(2)见解析
【解析】
(1)由表中数据即可求得各段范围内的概率,利用题中评判规则即可得解。
(2)由题意可知,样本中次品个数为6,突变品个数为2,“突变品”个数![]() 的可能取值为0,1,2.分别求出
的可能取值为0,1,2.分别求出![]() ,
,![]() ,
,![]() 的概率,问题得解。
的概率,问题得解。
(1)![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
因为设备的数据仅满足一个不等式,故其性能等级为丙.
(2)由题意可知,样本中次品个数为6,突变品个数为2,“突变品”个数![]() 的可能取值为0,1,2.
的可能取值为0,1,2.
![]() ,
,![]() ,
,![]() .
.
所以![]() 分布列为
分布列为
| 0 | 1 | 2 |
| | | |
![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目