题目内容
【题目】已知椭圆
的对称轴为坐标轴，焦点在
轴上，离心率为
，且经过点
.
（1）求椭圆的方程；
（2）设直线
与椭圆相交于
、
两点，且
，
，若原点
在以
为直径的圆外，求
的取值范围.
【答案】（1）
；（2）
【解析】
(1)由题意分别确定a,b的值，据此即可确定椭圆方程；
(2)联立直线方程与椭圆方程，直线与椭圆相交，则
，原点
在以
为直径的圆外，则
，据此结合韦达定理得到关于斜率的不等式，求解不等式即可确定
的取值范围.
（1）依题意，可设椭圆
的方程为
.
∵离心率为
，∴
，即
，∴
，
∵椭圆经过点
，∴
.
解得
，∴
，
，∴椭圆的方程为.
（2）记
、
两点坐标分别为
，
，
由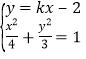
消去
，得
，
∵直线与椭圆有两个交点，
∴
，∴
，
由韦达定理
，
，
∵原点在以为直径的圆外，∴
为锐角，
∵
，
，
∴
为锐角，∴，
∵
.
∴
，∴
.
∵，∴
，
∴的取值范围为
.
【题目】某公司甲、乙两个班组分别试生产同一种规格的产品，已知此种产品的质量指标检测分数不小于70时，该产品为合格品，否则为次品，现随机抽取两个班组生产的此种产品各100件进行检测，其结果如下表：
质量指标检测分数 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
甲班组生产的产品件数 | 7 | 18 | 40 | 29 | 6 |
乙班组生产的产品件数 | 8 | 12 | 40 | 32 | 8 |
（1）根据表中数据，估计甲、乙两个班组生产该种产品各自的不合格率；
（2）根据以上数据，完成下面的2×2列联表，并判断是否有95％的把握认为该种产品的质量与生产产品的班组有关？
甲班组 | 乙班组 | 合计 | |
合格品 | |||
次品 | |||
合计 |
（3）若按合格与不合格比例，从甲班组生产的产品中抽取4件产品，从乙班组生产的产品中抽取5件产品，记事件A：从上面4件甲班组生产的产品中随机抽取2件，且都是合格品；事件B：从上面5件乙班组生产的产品中随机抽取2件，一件是合格品，一件是次品，试估计这两个事件哪一种情况发生的可能性大．
附：
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【题目】为评估
设备生产某种零件的性能，从该设备生产零件的流水线上随机抽取100件零件作为样本，测量其直径后，整理得到下表：
直径/ | 78 | 79 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 93 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算，样本的平均值
，标准差
，以频率值作为概率的估计值.
（1）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为
，并根据以下不等式进行评判（
表示相应事件的频率）：
①
；②
；③
，评判规则为：若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙；若仅满足其中一个，则等级为丙；若全部不满足，则等级为丁.试判断设备的性能等级.
（2）将直径小于等于
的零件或直径大于等于
的零件认定为是“次品”，将直径小于等于
的零件或直径大于等于
的零件认定为是“突变品”，从样本的“次品”中随意抽取2件零件，求“突变品”个数
的数学期望.
【题目】“开门大吉”是某电视台推出的游戏节目，选手面对1
号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，在一次场外调查中，发现参赛选手多数分为两个年龄段： 
； 
（单位：岁），其猜对歌曲名称与否的人数如图所示．
（Ⅰ）写出
列联表；判断是否有
的把握认为猜对歌曲名称是否与年龄有关；说明你的理由；（如表的临界值表供参考）
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
（Ⅱ）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，并抽取3名幸运选手，求3名幸运选手中恰好有一人在
岁之间的概率．
（参考公式： 
，其中
）
