题目内容
【题目】已知y=f(x)是定义域为R的奇函数,当x∈[0,+∞)时,f(x)=x(2﹣x),
(1)写出函数y=f(x)在x∈(﹣∞,0)时的解析式;
(2)若关于x的方程f(x)=a恰有两个不同的解,求a的值.
【答案】
(1)解:当x∈(﹣∞,0)时,﹣x∈(0,+∞),
∵y=f(x)是奇函数,
∴f(x)=﹣f(﹣x)=﹣[(﹣x)(2+x)]=x(x+2)
(2)解:由(1)得:f(x)= ![]() .
.
当x∈[0,+∞)时,f(x)=﹣x2+2x=﹣(x﹣1)2+1,最大值为1;
∴当x∈(﹣∞,0)时,f(x)=x2+2x=(x+1)2﹣1,最小值为﹣1.
∴据此可作出函数y=f(x)的图象,根据图象得,
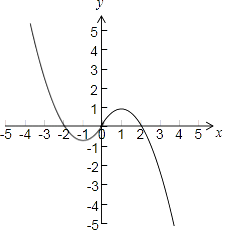
若方程f(x)=a恰有2个不同的解,则a=±1
【解析】(1)由奇函数的定义当x∈(﹣∞,0)时,﹣x∈(0,+∞)即f(x)=﹣f(﹣x)=x(x+2)。(2)根据题意得到分段函数,再利用二次函数的最值求出两个极值,故可得当f(x)=a恰有2个不同的解时a=±1
【考点精析】关于本题考查的函数奇偶性的性质,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能得出正确答案.

练习册系列答案
相关题目
【题目】已知如表为“五点法”绘制函数f(x)=Asin(ωx+φ)图象时的五个关键点的坐标(其中A>0,ω>0,|φ|<π)
x | ﹣ |
|
|
|
|
f(x) | 0 | 2 | 0 | ﹣2 | 0 |
(Ⅰ)请写出函数f(x)的最小正周期和解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
