题目内容
点P是圆 上的一个动点,过点P作PD垂直于
上的一个动点,过点P作PD垂直于 轴,垂足为D,Q为线段PD的中点。
轴,垂足为D,Q为线段PD的中点。
(1)求点Q的轨迹方程。
(2)已知点M(1,1)为上述所求方程的图形内一点,过点M作弦AB,若点M恰为弦AB的中点,求直线AB的方程。
 上的一个动点,过点P作PD垂直于
上的一个动点,过点P作PD垂直于 轴,垂足为D,Q为线段PD的中点。
轴,垂足为D,Q为线段PD的中点。(1)求点Q的轨迹方程。
(2)已知点M(1,1)为上述所求方程的图形内一点,过点M作弦AB,若点M恰为弦AB的中点,求直线AB的方程。
(1) ;(2)
;(2)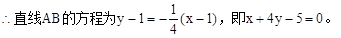
 ;(2)
;(2)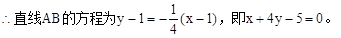
试题分析:(Ⅰ)设Q(x,y),P(x0,y0),则D(x0,0),由Q为线段PD的中点,知x0=x,y0=2y,由P(x0,y0)在圆x2+y2=16上,知x02+y02=16,由此能求出点Q的轨迹方程.
(Ⅱ)设直线AB的方程为y-1=k(x-1).由y=k(x-1)+1,
 ,得(1+4k2)x+8k(1-k)x+4(1-k)2-16=0,设A(x1,y1),B(x2,y2),x1+x2=
,得(1+4k2)x+8k(1-k)x+4(1-k)2-16=0,设A(x1,y1),B(x2,y2),x1+x2= 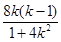 ,而M(1,1)是AB中点,则
,而M(1,1)是AB中点,则 =1,由此能求出直线方程.
=1,由此能求出直线方程.(1)设Q(
 ) P(
) P( ) 则D(
) 则D( )
)  即
即


 即
即 为所求。 …………4分
为所求。 …………4分(2)法1:依题意显然
 的斜率存在,设直线AB的斜率为k,则AB的方程可设为
的斜率存在,设直线AB的斜率为k,则AB的方程可设为 。
。由
 得
得
得
 …………7分
…………7分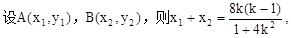

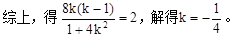 …………10分
…………10分 …………12分
…………12分法2:(直接求k):设A(x1,y1),B(x2,y2)。

 …………6分
…………6分 …………8分
…………8分
 …………10分
…………10分 …………12分
…………12分点评:解决该试题的关键是体现了解析几何中设而不求的解题思想,联立方程组,,转化为二次方程的根的问题,结合韦达定理得到。

练习册系列答案
相关题目
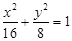 的焦点分别为
的焦点分别为 、
、 ,以原点为圆心且过焦点的圆O与椭圆相交于点
,以原点为圆心且过焦点的圆O与椭圆相交于点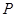 ,则
,则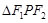 的面积等于( )
的面积等于( )



 上的一点
上的一点 ,它到椭圆的一个焦点
,它到椭圆的一个焦点 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点 的距离是( )
的距离是( )

 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 .  上一点
上一点 到它的右焦点距离为
到它的右焦点距离为 ,那么
,那么 
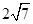


 为何值时,直线
为何值时,直线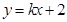 和曲线
和曲线 有两个公共点?有一个公共点?
有两个公共点?有一个公共点?



 的左焦点为
的左焦点为 ,
, 是两个顶点,如果
是两个顶点,如果 的距离等于
的距离等于 ,则椭圆的离心率为 .
,则椭圆的离心率为 .