题目内容
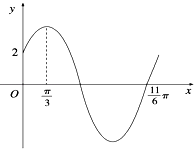
【题目】已知函数f(x)=sin(ωx+φ)﹣b(ω>0,0<φ<π)的图象两相邻对称轴之间的距离是 ![]() ,若将f(x)的图象先向右平移
,若将f(x)的图象先向右平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位,所得函数g(x)为奇函数.
个单位,所得函数g(x)为奇函数.
(1)求f(x)的解析式;
(2)求f(x)的对称轴及单调区间;
(3)若对任意x∈[0, ![]() ],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
],f2(x)﹣(2+m)f(x)+2+m≤0恒成立,求实数m的取值范围.
【答案】
(1)解:∵ ![]() ,∴ω=2∴f(x)=sin(2x+φ)﹣b.
,∴ω=2∴f(x)=sin(2x+φ)﹣b.
又 ![]() 为奇函数,且0<φ<π,则
为奇函数,且0<φ<π,则 ![]() ,
, ![]() ,故
,故 ![]()
(2)解:令2x+ ![]() =kπ+
=kπ+ ![]() ,求得
,求得 ![]() ,k∈Z,可得f(x)的图象的对称轴为
,k∈Z,可得f(x)的图象的对称轴为 ![]() ,k∈Z.
,k∈Z.
令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函数的增区间为
,可得函数的增区间为 ![]() .
.
令2kπ+ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ+
,求得kπ+ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,可得函数的减区间为
,可得函数的减区间为 ![]()
(3)解:由于 ![]() ,故
,故 ![]() ,∵f2(x)﹣(2+m)f(x)+2+m≤0恒成立,
,∵f2(x)﹣(2+m)f(x)+2+m≤0恒成立,
整理可得 ![]() .
.
由 ![]() ,得:
,得: ![]() ,故
,故 ![]() ,
,
即m取值范围是 ![]()
【解析】(1)利用正弦函数的周期性、奇偶性,求得ω和φ的值,可得f(x)的解析式.(2)利用正弦函数的单调性求得函数f(x)的单调区间.(3)利用正弦函数的定义域和值域,函数的恒成立问题,求得m的范围.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.

练习册系列答案
相关题目