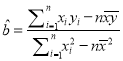题目内容
【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间. 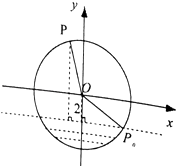
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
【答案】
(1)解:以O为原点建立如图所示的直角坐标系.
由于水轮绕着圆心O做匀速圆周运动,可设点P到水面的距离y(m)与时间t(s)满足函数关系 ![]() ,
,
∵水轮每分钟旋转4圈,
∴ ![]() .
.
∴ ![]() .
.
∵水轮半径为4 m,
∴A=4.
∴ ![]() .
.
当t=0时,y=0.
∴ ![]() .
.
∴ ![]() .
.
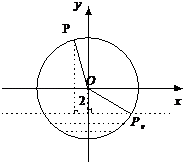
(2)解:由于最高点距离水面的距离为6,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
∴t=5+15k(k∈Z).
∴当k=0时,即t=5(s)时,点P第一次达到最高点.
【解析】(1)设点P到水面的距离y(m)与时间t(s)满足函数关系 ![]() ,利用周期求得ω,当t=0时,y=0,进而求得φ的值,则函数的表达式可得.(2)根据正弦函数的图象和性质可得t=5+15k(k∈Z)即当k=0时,即t=5(s)时,点P第一次达到最高点.
,利用周期求得ω,当t=0时,y=0,进而求得φ的值,则函数的表达式可得.(2)根据正弦函数的图象和性质可得t=5+15k(k∈Z)即当k=0时,即t=5(s)时,点P第一次达到最高点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目