题目内容
【题目】已知t>0,函数f(x)= 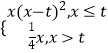 ,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是 .
,若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,则实数t的取值范围是 .
【答案】(3,4)
【解析】解:∵函数f(x)=  , ∴函数f′(x)=
, ∴函数f′(x)= 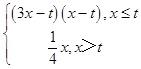 ,
,
当x< ![]() ,或x<t时,f′(x)>0,函数为增函数,
,或x<t时,f′(x)>0,函数为增函数,
当 ![]() <x<t时,f′(x)<0,函数为减函数,
<x<t时,f′(x)<0,函数为减函数,
故当x= ![]() 时,函数f(x)取极大值
时,函数f(x)取极大值 ![]() ,
,
函数f(x)有两个零点0和t,
若函数g(x)=f(f(x)﹣1)恰有6个不同的零点,
则方程f(x)﹣1=0和f(x)﹣1=t各有三个解,
即函数f(x)的图象与y=1和y=t+1各有三个零点,
由y|x=t= ![]() =
= ![]() ,
,
故  ,
,![]() =
= ![]() (t﹣3)(2t+3)2>0得:t>3,
(t﹣3)(2t+3)2>0得:t>3,
故不等式的解集为:t∈(3,4),
所以答案是:(3,4)

练习册系列答案
相关题目