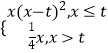题目内容
【题目】观察下列等式： （sin 
）﹣2+（sin 
）﹣2= 
×1×2；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+sin（ 
）﹣2= ×2×3；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+sin（ 
）﹣2= ×3×4；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+sin（ 
）﹣2= ×4×5；
…
照此规律，
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+（sin 
）﹣2= ．
【答案】
n（n+1）
【解析】解：观察下列等式： （sin 
）﹣2+（sin 
）﹣2= ×1×2；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+sin（ 
）﹣2= ×2×3；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+sin（ 
）﹣2= ×3×4；
（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+sin（ 
）﹣2= ×4×5；
…
照此规律（sin 
）﹣2+（sin 
）﹣2+（sin 
）﹣2+…+（sin 
）﹣2= ×n（n+1），
所以答案是： n（n+1）
【考点精析】解答此题的关键在于理解归纳推理的相关知识，掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理．
练习册系列答案
相关题目
