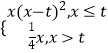Question

【题目】在平面直角坐标系xOy中，椭圆E： =1（a＞b＞0）的离心率为 ，两个顶点分别为A（﹣a，0），B（a，0），点M（﹣1，0），且3 = ，过点M斜率为k（k≠0）的直线交椭圆E于C，D两点，其中点C在x轴上方．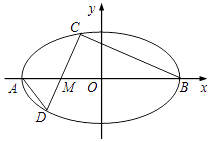
（1）求椭圆E的方程；
（2）若BC⊥CD，求k的值；
（3）记直线AD，BC的斜率分别为k1 ， k2 ， 求证： 为定值．

Answer 1

【答案】
（1）解：因为3 = ，所以3（﹣1+a，0）=（a+1，0），解得a=2．

又因为 = ，所以c= ，所以b2=a2﹣c2=1，

所以椭圆E的方程为 +y2=1．

（2）解：设点C的坐标为（x0，y0），y0＞0，

则 =（﹣1﹣x0，﹣y0）， =（2﹣x0，﹣y0）．

因为BC⊥CD，所以（﹣1﹣x0）（ 2﹣x0）+y02=0． ①

又因为 +y02=1，②

联立①②，解得x0=﹣ ，y0= ，

所以k= =2

（3）解：设C（x0，y0），则CD：y= （x+1）（﹣2＜x0＜2且x0≠﹣1），

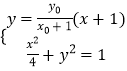由 消去y，

得x2+8y02x+4y02﹣4（x0+1）2=0．

又因为 +y02=1，所以得D（ ， ），

所以 = = 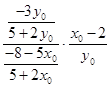=3，

所以 为定值．

【解析】（1）由3 = ，得a 即可；（2）设点C的坐标为（x0 ， y0），y0＞0，由BC⊥CD，得（﹣1﹣x0）（ 2﹣x0）+y02=0．解得x0=﹣ ，y0= ，即可．（3），设C（x0 ， y0），则CD：y= （x+1）（﹣2＜x0＜2且x0≠﹣1）， 由 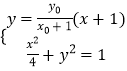消去y，得x2+8y02x+4y02﹣4（x0+1）2=0，得D（ ， ），可求 .