题目内容

已知在△ABC中，AD⊥BC于D，E是BC的中点，EF⊥BC交AB于点F，AB=8cm，BD=6cm，DC=4cm，求AF的长．
考点：三角形中的几何计算
专题：解三角形
分析：由题意作出图形，得到AD∥EF，利用平行线分线段成比例定理可求AF的长度．
解答： 解：如图

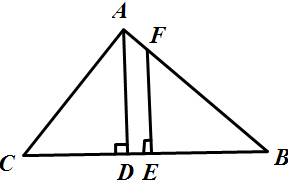
由题意，DE=BD-BE=
1
2
（6+4）-4=1，
因为AD⊥BC于D，E是BC的中点，EF⊥BC交AB于点F，
所以AD∥EF，
所以
BE
DE
=
BF
AF
，设AF=xcm，
5
1
=
8-x
x
，解得x=
4
3
．
点评：本题考查了三角形中平行线分线段成比例定理的运用，属于基础题．
练习册系列答案
相关题目
设函数f（x）的定义域为M，若函数f（x）满足条件[m，n]⊆M，使f（x）在[m，n]上的值域是[
m
2
，
n
2
]，则成f（x）为“半缩函数”，若函数f（x）=log3（3x+λ）为“半缩函数”，则λ的范围是（　　）
A、（0，1）
B、（0，
1
4
）
C、（0，
1
2
]
D、（
1
4
，+∞）
已知y=f（x+1）的定义域为[1，2]，求下列函数的定义域：
（1）f（x）；
（2）f（x-3）．
已知点P（4，3），保持点P与原点的距离不变，并绕原点分别旋转45°、120°、-45°到P1、P2、P3的位置，求点P1、P2、P3的坐标．
已知tanα=
3
，π＜α＜
3π
2
，求sinαcosα的值．
已知函数f（x）=x+
a
x
（a＞0）
（1）判断函数f（x）在（0，+∞）的单调性；
（2）若f（x）=x+
2b
x
在（0，4）上是减函数，在（4，+∞）上是增函数，求实数b的值；
（3）若c∈[1，4]，求函数f（x）=x+
c
x
在区间[1，2]上的最大值和最小值．
若p、q满足p-2q=1，直线px+3y+q=0必经过
 
点．
若函数f（x）=x3-mx2+mx+3m在（0，1）内有极大值，无极小值，则（　　）
A、m＜0B、m＜3
C、m＞3D、0＜m＜3
下列说法正确的是（　　）
A、在散点图中看不出两个变量是正相关还是负相关
B、回归方程得到的预报值是预报变量的精确值
C、回归方程一般都有时间性
D、相关系数r越接近0，说明两个变量的线性相关性越强

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网