题目内容
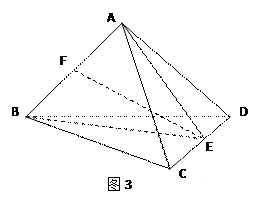
如图3:在空间四边形ABCD中,AC=AD,BC=BD,且E是CD的中点.
(1)求证:平面ABE 平面BCD;
平面BCD;
(2)若F是AB的中点,BC=AD,且AB=8,AE=10,求EF的长.
(1)求证:平面ABE
 平面BCD;
平面BCD;(2)若F是AB的中点,BC=AD,且AB=8,AE=10,求EF的长.
 |
(1)见解析(2)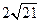
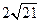
(1)证明:因为AC=AD,BC=BD,且E是CD的中点,所以BE CD,且AE
CD,且AE CD,
CD,
又AE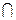 BE=E,所以CD
BE=E,所以CD 平面ABE,所以平面ABE
平面ABE,所以平面ABE 平面BCD
平面BCD
 (2)因为E是CD的中点,所以CE=ED,由(1)知BE
(2)因为E是CD的中点,所以CE=ED,由(1)知BE CD,且AE
CD,且AE CD,所以
CD,所以
BC2=BE2+CE2=BE2+ED2,AD2=AE2+ED2,因为BC=AD,所以AE = BE……3分
又因为F是AB的中点,所以AF=FB=4,且EF AB,所以EF=
AB,所以EF=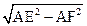
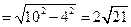
 CD,且AE
CD,且AE CD,
CD,又AE
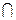 BE=E,所以CD
BE=E,所以CD 平面ABE,所以平面ABE
平面ABE,所以平面ABE 平面BCD
平面BCD  (2)因为E是CD的中点,所以CE=ED,由(1)知BE
(2)因为E是CD的中点,所以CE=ED,由(1)知BE CD,且AE
CD,且AE CD,所以
CD,所以BC2=BE2+CE2=BE2+ED2,AD2=AE2+ED2,因为BC=AD,所以AE = BE……3分
又因为F是AB的中点,所以AF=FB=4,且EF
 AB,所以EF=
AB,所以EF=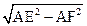

练习册系列答案
相关题目
 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD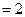 , AD=1, EF=
, AD=1, EF=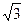 .
.
 平面FCB;
平面FCB;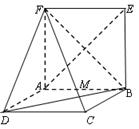

 所在平面与平面四边形
所在平面与平面四边形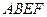 所在平面互相垂直,△
所在平面互相垂直,△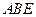 是等腰直角三角形,
是等腰直角三角形,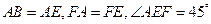 。
。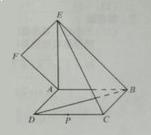
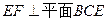 ;
;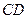 的中点为
的中点为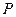 ,在直线
,在直线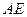 上是否存在一点
上是否存在一点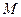 ,使得
,使得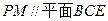 ?若存在,请指出点
?若存在,请指出点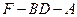 的大小。
的大小。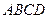 为菱形,
为菱形,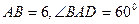 ,两个正三棱锥
,两个正三棱锥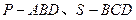 (底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点
(底面是正三角形且顶点在底面上的射影是底面正三角形的中心)的侧棱长都相等,点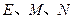 分别在
分别在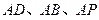 上,且
上,且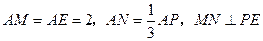 .
.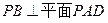 ;
;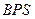 与底面
与底面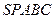 的体积.
的体积. 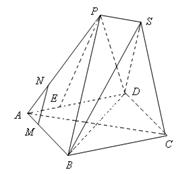
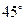 纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为
纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为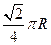 ,(R为地球半径),则A,B两点间的球面距离为__________________.
,(R为地球半径),则A,B两点间的球面距离为__________________.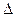 BCD的三条高线的交点;
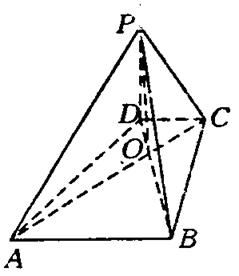
BCD的三条高线的交点;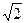 ,PB⊥PD.
,PB⊥PD.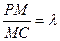 ,问
,问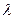 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.