题目内容
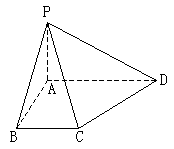
在正方体ABCD—A1B1C1D1中
(1)求证: BD⊥平面ACC1
(2)求二面角C1—BD—C的正切值
(1)求证: BD⊥平面ACC1
(2)求二面角C1—BD—C的正切值
 |
(1)见解析(2)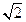
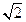
(1)证明:∵BD⊥AC,又∵CC1⊥CD, CC1⊥CB,
∴CC1⊥平面AC,∴CC1⊥BD,∴BD⊥平面ACC1
(2)解:连接AC,交BD于点O,则BD⊥ CO,连接C1 O,则
BD⊥C1 O,∴∠C O C1为所求二面角C1—BD—C的平面角,
在Rt△CC1O中,tan∠C O C1 =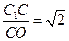
∴CC1⊥平面AC,∴CC1⊥BD,∴BD⊥平面ACC1
(2)解:连接AC,交BD于点O,则BD⊥ CO,连接C1 O,则
BD⊥C1 O,∴∠C O C1为所求二面角C1—BD—C的平面角,
在Rt△CC1O中,tan∠C O C1 =

练习册系列答案
相关题目
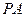 垂直于
垂直于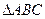 所在平面,
所在平面,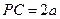 ,
,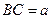 ,
,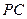 与平面
与平面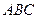 成
成 角,又
角,又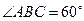 ,①求证:
,①求证: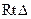 ;②求
;②求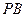 与平面
与平面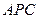 所成的角的正切值.
所成的角的正切值.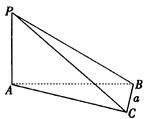
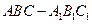 中,平面
中,平面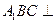 侧面。
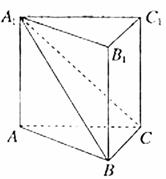
侧面。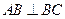 ;
;
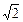 ,EF=EC=1,
,EF=EC=1, 
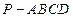 中,面
中,面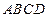 为矩形,
为矩形,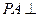 面
面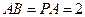
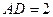 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;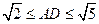 时,求二面角
时,求二面角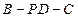 的取值范围。
的取值范围。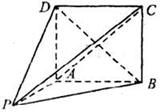
 平面BCD;
平面BCD;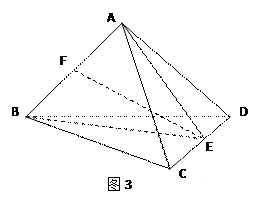
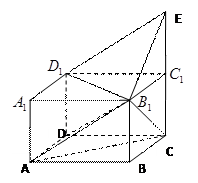
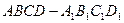 中,点
中,点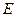 在棱
在棱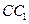 的延长线上,
的延长线上,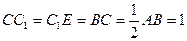 .
.
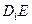 //平面
//平面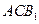 ;
; (Ⅱ) 求证:平面
(Ⅱ) 求证:平面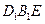
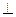 平面
平面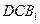 ;
;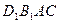 的体积.
的体积.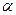 ⊥平面
⊥平面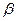 ,那么
,那么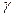 ,平面
,平面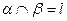 ,那么
,那么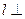 平面
平面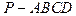 中,AD∥BC,∠ABC=90°,且
中,AD∥BC,∠ABC=90°,且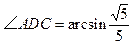 ,又PA⊥平面ABCD,AD=3AB=3PA=3a。
,又PA⊥平面ABCD,AD=3AB=3PA=3a。