题目内容
7.某高中从学生体能测试结果中随机抽取100名学生的测试结果,按体重(单位:kg)分组,得到的频率分布表如表所示.| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [50,55) | 5 | 0.050 |
| 第2组 | [55,60) | ① | 0.350 |
| 第3组 | [60,65) | 30 | ② |
| 第4组 | [65,70) | 20 | 0.200 |
| 第5组 | [70,75] | 10 | 0.100 |
| 合计 | 100 | 1.000 | |
(Ⅱ)从第3、4、5组中用分层抽样抽取6名学生进行第二次测试,求第3、4、5组每组各抽取多少名学生进入第二次测试?
(Ⅲ)在(Ⅱ)的前提下,在6名学生中随机抽取2名学生由李老师进行测试,求第4组至少有一名学生被李老师测试的概率?频率分布表.
分析 (Ⅰ)第2组的频数为35人,第3组的频数为$\frac{30}{100}$=$\frac{3}{10}$,
(Ⅱ)利用分层抽样得出3,4,5组分别抽取3人,2人,1人.
(Ⅲ)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第,5组的1位同学为C1,
运用列举从六为同学中抽2为同学有15种情况,运用古典概率的知识求解即可.
解答 解:(Ⅰ)由题意可知,第2组的频数为0.35×100=35人,
第3组的频数为$\frac{30}{100}$=$\frac{3}{10}$,
(Ⅱ)因为3,4,5组共有60名,所以利用分层抽样在60名学生中抽取6名学生,
每组分别为:第3组:$\frac{30}{60}$×6=3人,
第4组:$\frac{20}{60}$×6=2人,第5组:$\frac{10}{60}$×6=1人,
所以3,4,5组分别抽取3人,2人,1人,
(Ⅲ)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第,5组的1位同学为C1,
从六为同学中抽2为同学有:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),
(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),
(B1,B2),(B1,C1),(B2,C1)共
第4组至少有1位同学入选的有:(B1,B2),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),
(B1,C1),(B2,C1)共9种情况,
∴第4组至少有一名学生被李老师测试的概率$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题考查了运用列举法求解古典概率的方法,关键是运用统计中的抽样的方法得出数据,再按规律列举,不重复,不遗漏.

 阅读快车系列答案
阅读快车系列答案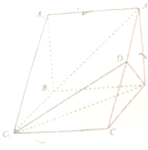 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点. 如图,三棱锥A-BCD中,已知:AB=AC=CD=DB=$\sqrt{3}$,BC=AD=2,求证:面ABC⊥面BCD.
如图,三棱锥A-BCD中,已知:AB=AC=CD=DB=$\sqrt{3}$,BC=AD=2,求证:面ABC⊥面BCD. 如图,AB为圆O的直径,PB,PC分别与圆O相切于B,C两点,延长BA,PC相交于点D.
如图,AB为圆O的直径,PB,PC分别与圆O相切于B,C两点,延长BA,PC相交于点D.