题目内容
15.已知(1-2x)7=a0+a1x+a2x2+a3x3+…+a7x7,求:(1)a1+a2+…+a7;
(2)a1+a2+a5+a7.
(3)a0+a2+a4+a6
(4)|a0|+|a1|+…+|a7|.
分析 (1)在所给的等式中,分别令x=0、x=1,从而求得a1+a2+…+a7 的值.
(2)利用通项公式求得a3 和a4 的值,可得a3+a4 的值,从而求得a1+a2+a5+a7的值.
(3)在所给的等式中,分别令x=1、x=-1,即可求得a0+a2+a4+a6 的值.
(4)由题意可得,|a0|+|a1|+…+|a7|即为(1+2x)7的展开式中各项的系数和,从而得出结论.
解答 解:(1)在(1-2x)7=a0+a1x+a2x2+a3x3+…+a7x7中,
令x=0可得a0=1.
令x=1可得a0+a1+a2+…+a7 =-1 ①,∴a1+a2+…+a7 =-2.
(2)由题意可得a3=${C}_{7}^{3}$•(-2)3=-280,a4=${C}_{7}^{4}$•(-2)4=560,
∴a3+a4=280,a1+a2+a5+a7 =(a1+a2+…+a7)-(a3+a4 )=-1-280=-281.
(3)在所给的等式中,令x=-1可得a0-a1+a2-a3+…-a7 =37 ②,
∴由①②可得 a0+a2+a4+a6 =$\frac{{3}^{7}-1}{2}$.
(4)由题意可得,|a0|+|a1|+…+|a7|.即(1+2x)7的展开式中各项的系数和,为37.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.某高中从学生体能测试结果中随机抽取100名学生的测试结果,按体重(单位:kg)分组,得到的频率分布表如表所示.
(Ⅰ)请求出频率分布表中①、②位置相应的数据;
(Ⅱ)从第3、4、5组中用分层抽样抽取6名学生进行第二次测试,求第3、4、5组每组各抽取多少名学生进入第二次测试?
(Ⅲ)在(Ⅱ)的前提下,在6名学生中随机抽取2名学生由李老师进行测试,求第4组至少有一名学生被李老师测试的概率?频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [50,55) | 5 | 0.050 |
| 第2组 | [55,60) | ① | 0.350 |
| 第3组 | [60,65) | 30 | ② |
| 第4组 | [65,70) | 20 | 0.200 |
| 第5组 | [70,75] | 10 | 0.100 |
| 合计 | 100 | 1.000 | |
(Ⅱ)从第3、4、5组中用分层抽样抽取6名学生进行第二次测试,求第3、4、5组每组各抽取多少名学生进入第二次测试?
(Ⅲ)在(Ⅱ)的前提下,在6名学生中随机抽取2名学生由李老师进行测试,求第4组至少有一名学生被李老师测试的概率?频率分布表.
4.某学校对学生进行三项身体素质测试,每项测试的成绩有3分、2分、1分,若各项成绩均不小于2分切三项测试分数之和不小于7分的学生,则其身体素质等级记为优秀;若三项测试分数之和小于6分,则该学生身体素质等级记为不合格,随机抽取10名学生的成绩记录如下表:
(1)利用上表提供的数据估算该学校学生身体素质的优秀率;
(2)从表中身体素质等级记为不合格的学生中任意抽取2人组成小组加强锻炼,求这2人三项测试总分相同的概率.
| 学生编号 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 |
| 三项成绩 | 2,1,2 | 1,2,2 | 2,3,2 | 3,1,1 | 3,2,2 | 2,3,1 | 3,3,3 | 1,1,1 | 3,3,1 | 2,2,2 |
(2)从表中身体素质等级记为不合格的学生中任意抽取2人组成小组加强锻炼,求这2人三项测试总分相同的概率.
5.已知P为抛物线C:y2=8x准线上任意一点,A(1,3)、B(1,-3),则△PAB的面积为( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
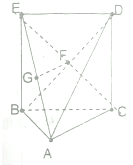 如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.
如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.