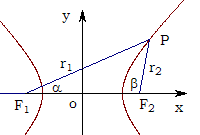
题目内容
过点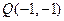 作已知直线
作已知直线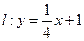 的平行线,交双曲线
的平行线,交双曲线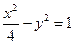 于点
于点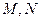 .
.
(1)证明:点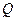 是线段
是线段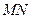 的中点.
的中点.
(2)分别过点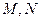 作双曲线的切线
作双曲线的切线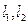 ,证明:三条直线
,证明:三条直线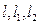 相交于同一点.
相交于同一点.
(3)设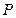 为直线
为直线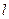 上一动点,过点
上一动点,过点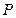 作双曲线的切线
作双曲线的切线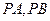 ,切点分别为
,切点分别为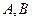 .证明:点
.证明:点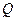 在直线AB上.
在直线AB上.
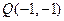 作已知直线
作已知直线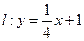 的平行线,交双曲线
的平行线,交双曲线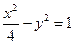 于点
于点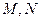 .
.(1)证明:点
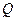 是线段
是线段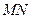 的中点.
的中点.(2)分别过点
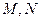 作双曲线的切线
作双曲线的切线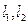 ,证明:三条直线
,证明:三条直线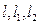 相交于同一点.
相交于同一点.(3)设
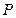 为直线
为直线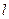 上一动点,过点
上一动点,过点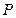 作双曲线的切线
作双曲线的切线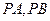 ,切点分别为
,切点分别为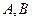 .证明:点
.证明:点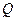 在直线AB上.
在直线AB上.证明略
(1)直线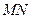 的方程为
的方程为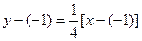 ,即
,即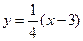 ,代入双曲线方程
,代入双曲线方程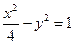 ,得
,得 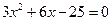 .
.
设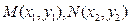 ,则
,则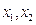 是方程的两根,所以
是方程的两根,所以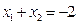 ,
,
于是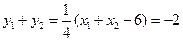 ,故点
,故点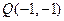 是线段
是线段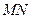 的中点. ………5分
的中点. ………5分
(2)双曲线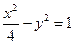 的过点
的过点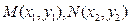 的切线方程分别为
的切线方程分别为
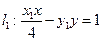 ,
,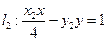 .
.
联立,得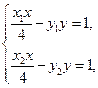 两式相加,并将
两式相加,并将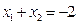 ,
,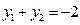 代入,得
代入,得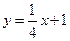 ,这说明直线
,这说明直线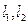 的交点在直线
的交点在直线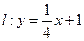 上,即三条直线
上,即三条直线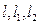 相交于同一点. …………………………10分
相交于同一点. …………………………10分
(3)设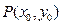 ,
,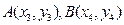 ,则
,则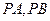 的方程分别为
的方程分别为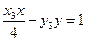 和
和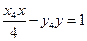 ,因为点
,因为点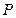 在两条直线上,所以
在两条直线上,所以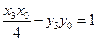 ,
, ,这表明点
,这表明点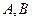 都在直线
都在直线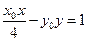 上,即直线
上,即直线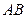 的方程为
的方程为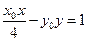 .
.
又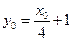 ,代入整理得
,代入整理得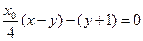 ,显然,无论
,显然,无论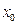 取什么值(即无论
取什么值(即无论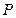 为直线
为直线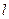 上哪一点),点
上哪一点),点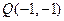 都在直线AB上. …………………………20分
都在直线AB上. …………………………20分
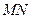 的方程为
的方程为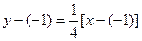 ,即
,即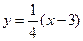 ,代入双曲线方程
,代入双曲线方程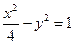 ,得
,得 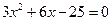 .
.设
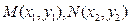 ,则
,则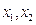 是方程的两根,所以
是方程的两根,所以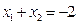 ,
,于是
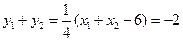 ,故点
,故点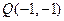 是线段
是线段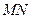 的中点. ………5分
的中点. ………5分(2)双曲线
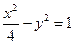 的过点
的过点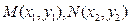 的切线方程分别为
的切线方程分别为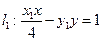 ,
,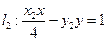 .
.联立,得
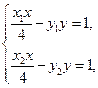 两式相加,并将
两式相加,并将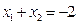 ,
,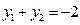 代入,得
代入,得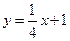 ,这说明直线
,这说明直线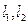 的交点在直线
的交点在直线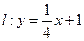 上,即三条直线
上,即三条直线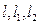 相交于同一点. …………………………10分
相交于同一点. …………………………10分(3)设
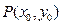 ,
,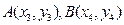 ,则
,则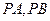 的方程分别为
的方程分别为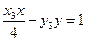 和
和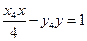 ,因为点
,因为点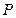 在两条直线上,所以
在两条直线上,所以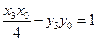 ,
, ,这表明点
,这表明点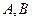 都在直线
都在直线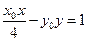 上,即直线
上,即直线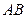 的方程为
的方程为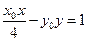 .
.又
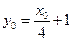 ,代入整理得
,代入整理得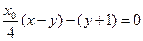 ,显然,无论
,显然,无论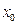 取什么值(即无论
取什么值(即无论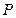 为直线
为直线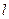 上哪一点),点
上哪一点),点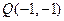 都在直线AB上. …………………………20分
都在直线AB上. …………………………20分
练习册系列答案
相关题目
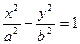 的左焦点为
的左焦点为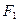 ,顶点为
,顶点为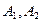 ,
,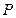 是该双曲线右支上任意一点,则分别以线段
是该双曲线右支上任意一点,则分别以线段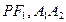 为直径的两圆一定( )
为直径的两圆一定( )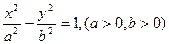 的离心率为e,过双曲线的右焦点且斜率为
的离心率为e,过双曲线的右焦点且斜率为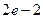
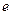 的取值范围是( )
的取值范围是( )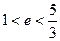
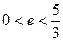
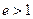
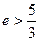
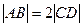 ,点E分有向线段
,点E分有向线段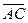 所成的比为
所成的比为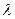 ,双曲线过C、D、E三点,且以A、B为焦点,当
,双曲线过C、D、E三点,且以A、B为焦点,当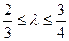 时,求双曲线离心率
时,求双曲线离心率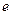 的取值范围.
的取值范围.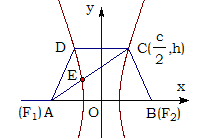
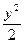 =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.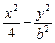 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.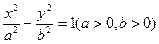 左支上的一点,F1、F2分别是左、右焦点,且焦距为2c,则
左支上的一点,F1、F2分别是左、右焦点,且焦距为2c,则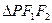 的内切圆的圆心的横坐标为( )
的内切圆的圆心的横坐标为( )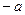
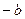
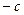
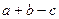
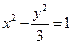 ,双曲线存在关于直线
,双曲线存在关于直线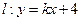 对称的点,求实数
对称的点,求实数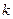 的取值范围。
的取值范围。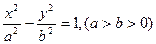 上异于顶点的任一点,双曲线的焦点为
上异于顶点的任一点,双曲线的焦点为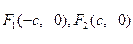 ,设
,设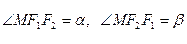 ,求
,求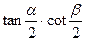 的值.
的值.