题目内容
设A、B是双曲线x2–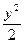 =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.
(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
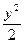 =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.(1)求直线AB的方程;
(2)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
(1)AB∶y=x+1(2)A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
(1)设AB∶y=k(x–1)+2代入x2–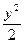 =1.
=1.
整理得(2–k2)x2–2k(2–k)x–(2–k)2–2="0 " ①
设A(x1,y1)、B(x2,y2),x1,x2为方程①的两根
所以2–k2≠0且x1+x2=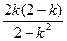 . 又N为AB中点,
. 又N为AB中点,
有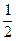 (x1+x2)=1.∴k(2–k)=2–k2,解得k="1." 故AB∶y=x+1.
(x1+x2)=1.∴k(2–k)=2–k2,解得k="1." 故AB∶y=x+1.
(2)解出A(–1,0)、B(3,4)得CD的方程为y=3–x 与双曲线方程联立.消y有x2+6x–11="0 " ②
与双曲线方程联立.消y有x2+6x–11="0 " ②
记C(x3,y3)、D(x4,y4)及CD中点M(x0,y0)由韦达定理可得x0=–3,y0=6.
∵|CD|=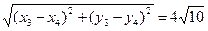
∴|MC|=|MD|=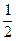 |CD|=2
|CD|=2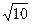 .
.
又|MA|=|MB|=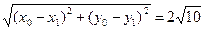 . 即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
. 即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
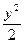 =1.
=1.整理得(2–k2)x2–2k(2–k)x–(2–k)2–2="0 " ①
设A(x1,y1)、B(x2,y2),x1,x2为方程①的两根
所以2–k2≠0且x1+x2=
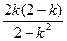 . 又N为AB中点,
. 又N为AB中点,有
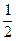 (x1+x2)=1.∴k(2–k)=2–k2,解得k="1." 故AB∶y=x+1.
(x1+x2)=1.∴k(2–k)=2–k2,解得k="1." 故AB∶y=x+1.(2)解出A(–1,0)、B(3,4)得CD的方程为y=3–x
 与双曲线方程联立.消y有x2+6x–11="0 " ②
与双曲线方程联立.消y有x2+6x–11="0 " ②记C(x3,y3)、D(x4,y4)及CD中点M(x0,y0)由韦达定理可得x0=–3,y0=6.
∵|CD|=
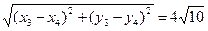
∴|MC|=|MD|=
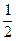 |CD|=2
|CD|=2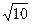 .
.又|MA|=|MB|=
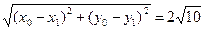 . 即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆.
. 即A、B、C、D四点到点M的距离相等,所以A、B、C、D四点共圆. 
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
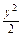 =1于A、B两点,且
=1于A、B两点,且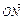 =
=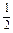 (
(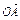 +
+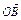 ).
).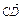 ·
·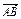 =0,那么A、B、C、D四点是否共圆?为什么?
=0,那么A、B、C、D四点是否共圆?为什么?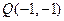 作已知直线
作已知直线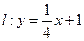 的平行线,交双曲线
的平行线,交双曲线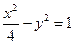 于点
于点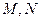 .
.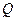 是线段
是线段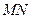 的中点.
的中点.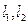 ,证明:三条直线
,证明:三条直线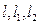 相交于同一点.
相交于同一点.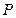 为直线
为直线 上一动点,过点
上一动点,过点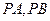 ,切点分别为
,切点分别为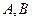 .证明:点
.证明:点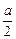 ,0),C(
,0),C(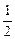 sinA,则动点A的轨迹方程为_________.
sinA,则动点A的轨迹方程为_________.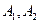 ,垂直于双曲线实轴的直线与双曲线交于
,垂直于双曲线实轴的直线与双曲线交于 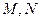 两点,则
两点,则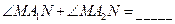
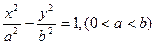 的半焦距为
的半焦距为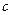 ,直线
,直线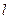 过点
过点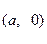 ,
,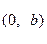 两点.已知原点到直线
两点.已知原点到直线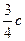 ,则双曲线的离心率为————
,则双曲线的离心率为————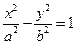
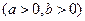 的一个焦点作圆
的一个焦点作圆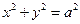 的两条切线,切点分别为A,B,若
的两条切线,切点分别为A,B,若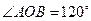 (O是坐标原点),则双曲线线C的离心率为 .
(O是坐标原点),则双曲线线C的离心率为 .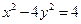 的两准线之间的距离是 。
的两准线之间的距离是 。