题目内容
已知向量m=( sin
sin  ,1),n=(cos
,1),n=(cos  ,cos2
,cos2 ).记f(x)=m·n.
).记f(x)=m·n.
(1)若f(α)= ,求cos(
,求cos(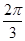 -α)的值;
-α)的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cos B=bcos C,若f(A)= ,试判断△ABC的形状.
,试判断△ABC的形状.
 sin
sin  ,1),n=(cos
,1),n=(cos  ,cos2
,cos2 ).记f(x)=m·n.
).记f(x)=m·n.(1)若f(α)=
 ,求cos(
,求cos(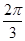 -α)的值;
-α)的值;(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a-c)cos B=bcos C,若f(A)=
 ,试判断△ABC的形状.
,试判断△ABC的形状.(1)1 (2)等边三角形
f(x)= sin
sin  cos
cos  +cos2
+cos2 =
= sin
sin +
+ cos
cos +
+ =sin(
=sin( +
+ )+
)+ .
.
(1)由已知f(α)= 得sin(
得sin( +
+ )+
)+ =
= ,
,
于是 +
+ =2kπ+
=2kπ+ ,k∈Z,即α=4kπ+
,k∈Z,即α=4kπ+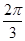 ,k∈Z,
,k∈Z,
∴cos(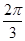 -α)=cos(
-α)=cos(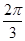 -4kπ-
-4kπ-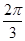 )=1.
)=1.
(2)根据正弦定理知:
(2a-c)cos B=bcos C⇒(2sin A-sin C)cos B=sin Bcos C⇒2sin Acos B=sin(B+C)=sin A⇒cos B= ⇒B=
⇒B=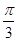 ,
,
∵f(A)= ,
,
∴sin( +
+ )+
)+ =
= ⇒
⇒ +
+ =
=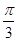 或
或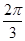 ⇒A=
⇒A=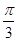 或π,而0<A<
或π,而0<A<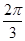 ,
,
所以A=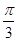 ,因此△ABC为等边三角形.
,因此△ABC为等边三角形.
 sin
sin  cos
cos  +cos2
+cos2 =
= sin
sin +
+ cos
cos +
+ =sin(
=sin( +
+ )+
)+ .
.(1)由已知f(α)=
 得sin(
得sin( +
+ )+
)+ =
= ,
,于是
 +
+ =2kπ+
=2kπ+ ,k∈Z,即α=4kπ+
,k∈Z,即α=4kπ+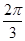 ,k∈Z,
,k∈Z,∴cos(
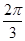 -α)=cos(
-α)=cos(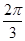 -4kπ-
-4kπ-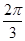 )=1.
)=1.(2)根据正弦定理知:
(2a-c)cos B=bcos C⇒(2sin A-sin C)cos B=sin Bcos C⇒2sin Acos B=sin(B+C)=sin A⇒cos B=
 ⇒B=
⇒B=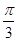 ,
,∵f(A)=
 ,
,∴sin(
 +
+ )+
)+ =
= ⇒
⇒ +
+ =
=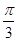 或
或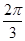 ⇒A=
⇒A=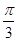 或π,而0<A<
或π,而0<A<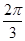 ,
,所以A=
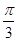 ,因此△ABC为等边三角形.
,因此△ABC为等边三角形.
练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 中,若
中,若 ,则
,则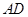 为半圆的直径,
为半圆的直径,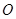 为半圆的圆心,
为半圆的圆心,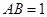 ,
,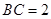 ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形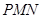 ,使得
,使得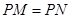 ,
,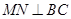 .
.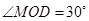 ,求三角形铁皮
,求三角形铁皮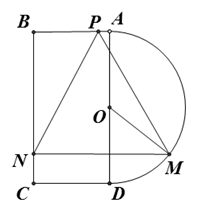
 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.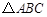 中,
中,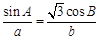 .
. 的值;
的值; ,求
,求 ,求它水平放置时的直观图的面积 .
,求它水平放置时的直观图的面积 .