题目内容
【题目】定义 
为n个正数p1 ， p2 ， …，pn的“均倒数”，若已知数列{an}，的前n项的“均倒数”为 
，又bn= 
，则 
+ 
+…+ 
=（ ）
A.
B.
C.
D.
【答案】C
【解析】解：∵数列{an}的前n项的“均倒数”为 
，
∴ 
= ，∴ 
，
∴a1=S1=5，
n≥2时，an=Sn﹣Sn﹣1=（5n2）﹣[5（n﹣1）2]=10n﹣5，
n=1时，上式成立，
∴an=10n﹣5，
∴bn= 
=2n﹣1， 
= 
= 
（ 
），
∴ 
+ 
+…+ 
= （1﹣ 
+…+ 
）
= 
= 
．
故选：C．
【考点精析】利用数列的前n项和对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系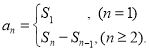
．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
【题目】某校高三2班有48名学生进行了一场投篮测试，其中男生28人，女生20人．为了了解其投篮成绩，甲、乙两人分别对全班的学生进行编号（1~48号），并以不同的方法进行数据抽样，其中一人用的是系统抽样，另一人用的是分层抽样．若此次投篮考试的成绩大于或等于80分视为优秀，小于80分视为不优秀，以下是甲、乙两人分别抽取的样本数据：
（Ⅰ）从甲抽取的样本数据中任取两名同学的投篮成绩，记“抽到投篮成绩优秀”的人数为X，求X的分布列和数学期望；
（Ⅱ）请你根据乙抽取的样本数据完成下列2×2列联表，判断是否有95%以上的把握认为投篮成绩和性别有关？
（Ⅲ）判断甲、乙各用何种抽样方法，并根据（Ⅱ）的结论判断哪种抽样方法更优？说明理由.
下面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（参考公式：
，其中
）
