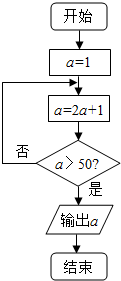
题目内容
8．已知函数f（x）=sin4x-cos4x，则f（x）的最小正周期是（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
分析 利用三角函数的运算，将函数进行化简，结合三角函数的周期公式进行求解即可．
解答 解：f（x）=sin4x-cos4x=（sin2x-cos2x）（sin2x+cos2x）
=sin2x-cos2x=-cos2x，
则函数的周期T=$\frac{2π}{2}=π$，
故选：B．
点评 本题主要考查三角函数的周期的计算，将函数进行化简是解决本题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
18．已知定义在R上的函数f（x）满足如下条件：①函数f（x）的图象关于y轴对称；②对于任意x∈R，f（2+x）-f（2-x）=0；③当x∈[0，2]时，f（x）=x．若过点（-1，0）的直线l与函数y=f（x）的图象在x∈[0，16]上恰有8个交点，在直线l斜率k的取值范围是（ ）
| A． | （$\frac{2}{19}$，$\frac{2}{15}$） | B． | （0，$\frac{15}{2}$） | C． | （0，$\frac{2}{17}$） | D． | （0，$\frac{17}{2}$） |
3．计算$\frac{i}{1-i}$=-（ ）
| A． | $\frac{-1+i}{2}$ | B． | $\frac{-1-i}{2}$ | C． | $\frac{1-i}{2}$ | D． | $\frac{1+i}{2}$ |
17．
如图所示，将n2（n≥9）个正数排成n行n列的数阵，其中的每一行都成等差数列，每一列都成等比数列，各等比数列的公比都相同且不为1，若a11=a22=a34=$\frac{1}{2}$，则a11+a22+a33+…+a99=（ ）
如图所示，将n2（n≥9）个正数排成n行n列的数阵，其中的每一行都成等差数列，每一列都成等比数列，各等比数列的公比都相同且不为1，若a11=a22=a34=$\frac{1}{2}$，则a11+a22+a33+…+a99=（ ）| A． | $\frac{1031}{512}$ | B． | $\frac{1031}{512}$ | C． | $\frac{1013}{1024}$ | D． | $\frac{1031}{1024}$ |