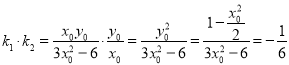题目内容
【题目】定义域为
的函数
图像的两个端点为
、
，向量
，
是
图像上任意一点，其中
，若不等式
恒成立，则称函数在上满足“
范围线性近似”，其中最小正实数称为该函数的线性近似阈值.若函数
定义在
上，则该函数的线性近似阈值是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
由向量
及
可得：
两点的横坐标相等，将不等式
恒成立问题转化成：
时，
恒成立，转化成：
.，记：
，即可求得
，问题得解。
作出函数
图像，它的图象在上的两端点分别为：
,
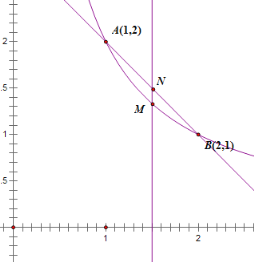
所以直线
的方程为：
设
是曲线上的一点，
，其中
由，可知
三点共线，
所以
点的坐标满足直线的方程，
又
,
,则
所以两点的横坐标相等.
故
函数在上满足“
范围线性近似”
所以 时，恒成立.
即：恒成立.
记，整理得：
，
，当且仅当
时，等号成立。
当
时，
所以，所以
.
即：
所以该函数的线性近似阈值是：
故选：B
练习册系列答案
相关题目
