题目内容
【题目】已知直线![]() 经过椭圆
经过椭圆![]() (
(![]() )的左顶点
)的左顶点![]() 和
和
上顶点![]() .椭圆
.椭圆![]() 的右顶点为
的右顶点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,直线
轴上方的动点,直线![]() 、
、![]() 与直线
与直线![]()
![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求线段![]() 长度的最小值;
长度的最小值;
(Ⅲ)当线段![]() 的长度最小时,椭圆
的长度最小时,椭圆![]() 上是否存在这样的点
上是否存在这样的点![]() ,使得
,使得![]() 的面积为
的面积为![]() ?若存在,确定点
?若存在,确定点![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)椭圆
(Ⅲ)椭圆![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 的面积为
的面积为![]() .
.
【解析】
(Ⅰ)令![]() 得
得![]() ,所以
,所以![]() ,所以
,所以![]() ,令
,令![]() 得
得![]() ,所以
,所以![]() ,所以
,所以
![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(Ⅱ)显然直线![]() 的斜率存在且为正数,设直线
的斜率存在且为正数,设直线![]() 的方程为
的方程为![]() (
(![]() ),联立得
),联立得
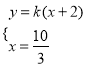 ,解得
,解得![]() ,由
,由![]() 得
得![]() ,
,
显然![]() ,由求根公式得
,由求根公式得![]() 或
或![]() (舍),所以
(舍),所以![]() ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,联立得
,联立得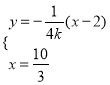 ,解得
,解得![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”,因此,线段
”,因此,线段![]() 长度的最小值为
长度的最小值为![]() ;
;
(Ⅲ)由(Ⅱ)知,![]() 时线段
时线段![]() 的长度最小,此时
的长度最小,此时![]() ,
,![]() ,因为
,因为![]() 的面积为
的面积为![]()
![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为直线
,因为直线![]() 的方程为
的方程为![]() ,设过点
,设过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程为
的方程为![]()
![]() ,由两平行线之间距离为
,由两平行线之间距离为![]() 得
得![]() ,解得
,解得![]() 或
或![]() ,当
,当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,联立得
,联立得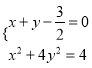 ,消去
,消去![]() 得
得![]() ,显然判别式
,显然判别式![]() ,故点
,故点![]() 有
有![]() 个;当
个;当![]() 时,直线
时,直线
![]() 的方程为
的方程为![]() ,联立得
,联立得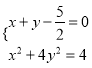 ,消去
,消去![]() 得
得![]() ,显然判别式
,显然判别式![]() ,故
,故
点![]() 不存在.所以,椭圆
不存在.所以,椭圆![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 的面积为
的面积为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某数学小组到进行社会实践调查,了解鑫鑫桶装水经营部在为如何定价发愁。进一步调研了解到如下信息:该经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表:
销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
根据以上信息,你认为该经营部定价为多少才能获得最大利润?( )
A.每桶8.5元B.每桶9.5元C.每桶10.5元D.每桶11.5元