题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)将![]() 代入函数
代入函数![]() 的解析式,利用导数可得出函数
的解析式,利用导数可得出函数![]() 的单调区间;
的单调区间;
(2)求函数![]() 的导数,分类讨论
的导数,分类讨论![]() 的范围,利用导数分析函数
的范围,利用导数分析函数![]() 的单调性,求出函数
的单调性,求出函数![]() 的最值可判断
的最值可判断![]() 是否恒成立,可得实数
是否恒成立,可得实数![]() 的取值范围.
的取值范围.
(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,此时,函数
,此时,函数![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,则
,则![]() ,此时,函数
,此时,函数![]() 为增函数.
为增函数.
所以,函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
(2)![]() ,则
,则![]() ,
,
![]()
![]() .
.
①当![]() 时,即当
时,即当![]() 时,
时,![]() ,
,
由![]() ,得
,得![]() ,此时,函数
,此时,函数![]() 为增函数;
为增函数;
由![]() ,得
,得![]() ,此时,函数
,此时,函数![]() 为减函数.
为减函数.
则![]() ,不合乎题意;
,不合乎题意;
②当![]() 时,即
时,即![]() 时,
时,
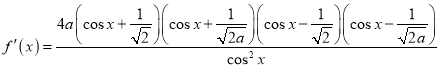 .
.
不妨设![]() ,其中
,其中![]() ,令
,令![]() ,则
,则![]() 或
或![]() .
.
(i)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,此时,函数
,此时,函数![]() 为增函数.
为增函数.
此时![]() ,
,
而![]() ,
,
构造函数![]() ,
,![]() ,则
,则![]() ,
,
所以,函数![]() 在区间
在区间![]() 上单调递增,则
上单调递增,则![]() ,
,
即当![]() 时,
时,![]() ,所以,
,所以,![]() .
.
![]() ,符合题意;
,符合题意;
②当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,符合题意;
,符合题意;
③当![]() 时,同理可得函数
时,同理可得函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
此时![]() ,则
,则![]() ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】古人云:“腹有诗书气自华.”为响应全民阅读,建设书香中国,校园读书活动的热潮正在兴起.某校为统计学生一周课外读书的时间,从全校学生中随机抽取![]() 名学生进行问卷调査,统计了他们一周课外读书时间(单位:
名学生进行问卷调査,统计了他们一周课外读书时间(单位:![]() )的数据如下:
)的数据如下:
一周课外读书时间/ |
|
|
|
|
|
|
|
|
| 合计 |
频数 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
频率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根据表格中提供的数据,求![]() ,
,![]() ,
,![]() 的值并估算一周课外读书时间的中位数.
的值并估算一周课外读书时间的中位数.
(2)如果读书时间按![]() ,
,![]() ,
,![]() 分组,用分层抽样的方法从
分组,用分层抽样的方法从![]() 名学生中抽取20人.
名学生中抽取20人.
①求每层应抽取的人数;
②若从![]() ,
,![]() 中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
中抽出的学生中再随机选取2人,求这2人不在同一层的概率.
【题目】某学生社团对![]() 年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日
年元宵节当天游览磁器口古镇景区的游客满意度抽样调查,从当日![]() 万名游客中随机抽取
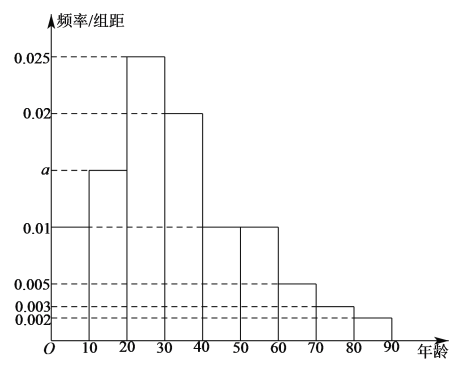
万名游客中随机抽取![]() 人进行统计,结果如下图的频率分布表和频率分布直方图:
人进行统计,结果如下图的频率分布表和频率分布直方图:
年龄 | 频数 | 频率 | 满意 | 不满意 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用频率分布直方图,估算游客的平均年龄和年龄的中位数;
(3)称年龄不低于![]() 岁的人群为“安逸人群”,完成
岁的人群为“安逸人群”,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为游客的满意度与“安逸人群”人数相关.
的把握认为游客的满意度与“安逸人群”人数相关.
|
| 合计 | |
满意 | |||
不满意 | |||
合计 |
参考公式: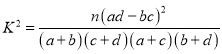 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.