Question

【题目】已知O为坐标原点，过点M（1，0）的直线l与抛物线C：y2＝2px（p＞0）交于A，B两点，且.

（1）求抛物线C的方程；

（2）过点M作直线l'⊥l交抛物线C于两点，记△OAB，△OPQ的面积分别为S1，S2，证明：为定值.

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）设直线的方程为，与抛物线的方程联立消去得关于的方程，利用根于系数的关系表示，从而求得的值；

（2）由题意求出弦长以及原点到直线的距离，计算△OAB的面积，同理求出△OPQ的面积，再求的值.

（1）解：设直线l的方程为：x＝my+1，

与抛物线C：y2＝2px（p＞0）联立，消去x得：

y2﹣2pmy﹣2p＝0；

设A（x1，y1），B（x2，y2），

则y1+y2＝2pm，y1y2═﹣2p；

由，得

x1x2+y1y2＝（my1+1）（my2+1）+y1y2

＝（1+m2）y1y2+（y1+y2）m+1

＝（1+m2）（﹣2p）+2pm2+1

＝﹣2p+1＝﹣3，

解得p＝2，

∴抛物线C的方程为y2＝4x；

（2）证明：由（1）知，点M（1，0）是抛物线C的焦点，

所以|AB|＝x1+x2+p＝my1+my2+2+p＝4m2+4，

又原点到直线l的距离为d，

所以△OAB的面积为S14（m2+1）＝2，

又直线l′过点M，且l'⊥l，

所以△OPQ的面积为S2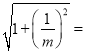＝22；

所以，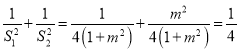

即为定值.