题目内容
【题目】已知椭圆C: ![]() (a>b>0),长轴长为4,离心率为
(a>b>0),长轴长为4,离心率为![]() .
.
(Ⅰ)椭圆的求椭圆的标准方程;
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围.
【答案】(Ⅰ) ![]() +y2=1(Ⅱ)k∈(-2,-
+y2=1(Ⅱ)k∈(-2,- ![]() )∪(
)∪(![]() ,2).
,2).
【解析】试题分析:(1)由题意可得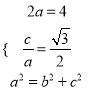 ,解得即可;
,解得即可;
(2)直线![]() 的方程为
的方程为![]() ,设
,设![]() .与椭圆方程联立,由
.与椭圆方程联立,由![]() ,解得
,解得![]() 的取值范围.可得根与系数的关系.若
的取值范围.可得根与系数的关系.若![]() 为锐角,则
为锐角,则![]() ,把根与系数的关系代入又得到
,把根与系数的关系代入又得到![]() 的取值范围,取其交集即可.
的取值范围,取其交集即可.
试题解析:(Ⅰ)依题意, 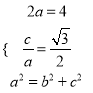 ,解得
,解得![]() ,
,
故椭圆C的方程为![]() +y2=1.
+y2=1.
(Ⅱ)如图,依题意,直线l的斜率必存在,
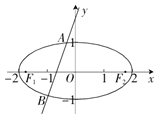
设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),
联立方程组 ,消去y整理得(1+4k2)x2+16kx+12=0,
,消去y整理得(1+4k2)x2+16kx+12=0,
由韦达定理,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=![]() +
+![]() +4=
+4=![]() ,
,
因为直线l与椭圆C相交,则Δ>0,
即256k2-48(1+4k2)>0,
解得k<-![]() 或k>
或k>![]() ,
,
当∠AOB为锐角时,向量![]() ,则x1x2+y1y2>0,
,则x1x2+y1y2>0,
即![]() +
+![]() >0,解得-2<k<2,
>0,解得-2<k<2,
故当∠AOB为锐角时,k∈(-2,- ![]() )∪(
)∪(![]() ,2).
,2).

练习册系列答案
相关题目