Question

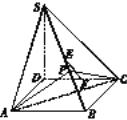
【题目】四棱锥S－ABCD中的底面是菱形，∠BAD＝60°，SD⊥底面ABCD，SD＝AB＝2，E、F分别为SB、CD的中点．

(Ⅰ)求证：EF∥平面SAD；

(Ⅱ)点P是SB上一点，若SB⊥平面APC，试确定点P的位置．

Answer 1

【答案】(1)见解析；(2) 当SP∶PB＝3∶1时，SB⊥平面APC.

【解析】试题分析：（Ⅰ）取SA的中点M，连接EM，DM，可证四边形EFDM是平行四边形，即可证明EF∥平面SAD；（Ⅱ）连接BD，由ABCD是菱形，AB＝2，∠BAD＝60°，可得BD，再由SD⊥底面ABCD，SD＝2，可得SB＝SC，取BC中点Q，连接SQ，作CP⊥SB于点P，可证得△BSQ∽△BCP，即可得SP∶PB，然后连接AP，可证AP⊥SB，即可证此时SB⊥平面APC.

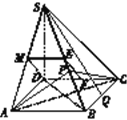
试题解析：(Ⅰ)证明：取SA的中点M，连接EM，DM

在△SAB中，EM∥AB，EM＝AB

又∵DF∥AB，DF＝AB

∴EM＝DF，EM∥DF

∴四边形EFDM是平行四边形

∴EF∥DM

又∵ EF平面SAD，DM平面SAD

∴ EF∥平面SAD

(Ⅱ)解：连接BD，因为ABCD是菱形，AB＝2，∠BAD＝60°，所以BD＝2，

因为SD⊥底面ABCD，SD＝2，所以，可得SB＝SC＝

在等腰三角形SBC中，取BC中点Q，连接SQ，作CP⊥SB于点P，

可证得△BSQ∽△BCP，所以，即，得

此时SP∶PB＝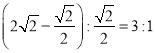

下面证明当SP∶PB＝3∶1时，SB⊥平面APC.

连接AP，易知△APB≌△CPB，所以∠APB＝∠CPB＝90°，即AP⊥SB，

又CP⊥SB，AP∩CP＝P，AP平面APC，CP平面APC，

所以SB⊥平面APC.

所以当SP∶PB＝3∶1时，SB⊥平面APC.