题目内容
(本题满分14分)已知数列 是首项
是首项 公比
公比 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足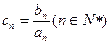 .
.
(1)求证: 是等差数列;
是等差数列;
(2)求数列 的前n项和Sn;
的前n项和Sn;
(3)若 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数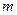 的取值范围。
的取值范围。
 是首项
是首项 公比
公比 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足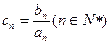 .
. (1)求证:
 是等差数列;
是等差数列; (2)求数列
 的前n项和Sn;
的前n项和Sn;(3)若
 对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数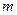 的取值范围。
的取值范围。解:(1)由题意知, , ………………1分
, ………………1分


∴数列 是首项
是首项 ,公差
,公差 的等差数列。……………3分
的等差数列。……………3分
(2)由(1)知,
 ,
,

 ①
①
 ② ①-②得
② ①-②得

 .
.  …………8分
…………8分
(3)

∴当n=1时, , 当
, 当 时,
时,
即 。
。
∴当n=2时, 取最大值是
取最大值是 。
。


即 得
得 或
或 。
。
故实数m的取值范围为 ……………14分
……………14分
 , ………………1分
, ………………1分

∴数列
 是首项
是首项 ,公差
,公差 的等差数列。……………3分
的等差数列。……………3分(2)由(1)知,

 ,
,
 ①
① ② ①-②得
② ①-②得
 .
.  …………8分
…………8分(3)


∴当n=1时,
 , 当
, 当 时,
时,
即
 。
。∴当n=2时,
 取最大值是
取最大值是 。
。

即
 得
得 或
或 。
。故实数m的取值范围为
 ……………14分
……………14分略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 n项和为Sn,且a3=5,S15="225."
n项和为Sn,且a3=5,S15="225." 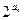 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 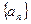 满足
满足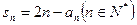 。
。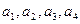 ,并由此猜想通项公式
,并由此猜想通项公式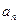 ;
;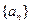 满足
满足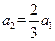 ,
,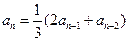 (
(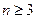 且
且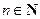 )
)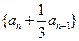 是常数列;
是常数列;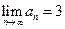 时,求数列
时,求数列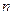 项和.
项和.
 的通项公式;
的通项公式;  ,求数列
,求数列
 ,
,
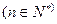 ,记
,记 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数 ;
; 满足
满足 则
则 的最小值为_________.
的最小值为_________. 的前
的前 项和
项和 ,利用倒序求和的方法得:
,利用倒序求和的方法得: ;类似的,记等比数列
;类似的,记等比数列 的前
的前 ,且
,且
 ,试类比等差数列求和的方法,可将
,试类比等差数列求和的方法,可将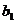 ,末项
,末项 与项数
与项数 _______________。
_______________。 的前n项和为
的前n项和为 ,且
,且 ,数列
,数列 为等差数列,且
为等差数列,且
 ,求数列
,求数列 的前n项和
的前n项和 。
。