题目内容
设数列
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列
(3)设 ,
,
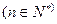 ,记
,记 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数 都有
都有 ;
;

(1)求数列
 的通项公式;
的通项公式; (2)设
 ,求数列
,求数列
(3)设
 ,
,
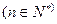 ,记
,记 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数 都有
都有 ;
;解:(1)
 是首项为
是首项为 的等比数列 2分
的等比数列 2分
 4分
4分
当 仍满足上式。
仍满足上式。

注:未考虑 的情况,扣1分。
的情况,扣1分。
(2)由(1)得,当 时,
时,
 8分
8分

 9分
9分
两式作差得 11分
11分


 13分
13分
(3)
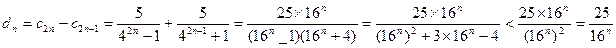 又
又 ,
,

当 时,
时, ,
,
当 时,
时,
 …………………14分
…………………14分

 是首项为
是首项为 的等比数列 2分
的等比数列 2分 4分
4分当
 仍满足上式。
仍满足上式。
注:未考虑
 的情况,扣1分。
的情况,扣1分。(2)由(1)得,当
 时,
时, 8分
8分
 9分
9分两式作差得
 11分
11分

 13分
13分(3)

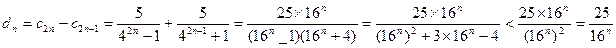 又
又 ,
,

当
 时,
时, ,
, 当
 时,
时, …………………14分
…………………14分略

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的前n项和为
的前n项和为 ,且满足
,且满足 ,则数列
,则数列
 是首项
是首项 公比
公比 的等比数列,设
的等比数列,设 ,数列
,数列 满足
满足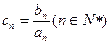 .
.  是等差数列;
是等差数列;  对一切正整数
对一切正整数 恒成立,求实数
恒成立,求实数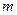 的取值范围。
的取值范围。 满足
满足

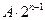


 ,把递推关系变成
,把递推关系变成
 后,就容易求出
后,就容易求出 存在吗?
存在吗? ,若不等式
,若不等式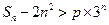 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
 }的通项公式。
}的通项公式。 ,数列{
,数列{ }的前n项和为
}的前n项和为 ,证明
,证明
 }的前
}的前 项和
项和 ,首项
,首项 ,公比
,公比 .
. ;
;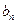 }满足
}满足 ,
, ,求数列{
,求数列{ ,记
,记 ,数列{
,数列{ }的前项和为
}的前项和为 ,求证:当
,求证:当 时,
时, .
.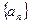 中,
中,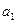 =2,
=2,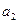 =3,其前
=3,其前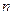 项和
项和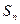 满足
满足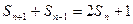
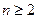 ,
, 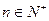 )。
)。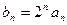 ,求数列
,求数列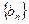 的前
的前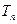 ;
; 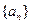 中,
中,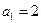 ,
,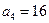 .
.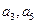 分别是等差数列
分别是等差数列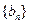 的第三项和第五项,试求数列
的第三项和第五项,试求数列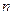 项和
项和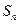 .
.