题目内容
【题目】如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
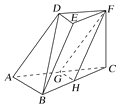
(1)求证:BD∥平面FGH;
(2)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45° ,求平面FGH与平面ACFD所成的角(锐角)的大小.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
试题解析:(Ⅰ)根据![]() 便可得到
便可得到![]() ,从而可以得出四边形
,从而可以得出四边形![]() 为平行四边形,从而得到
为平行四边形,从而得到![]() ,便有
,便有![]() 平面
平面![]() 再证明
再证明![]() 平面
平面![]() ,从而得到平面B
,从而得到平面B![]() 平面
平面![]() ,从而
,从而![]() 平面
平面![]() ;
;
(Ⅱ)连接![]() ,根据条件能够说明
,根据条件能够说明![]() 三直线两两垂直,从而分别以这三直线为
三直线两两垂直,从而分别以这三直线为![]() 轴,建立空间直角坐标系,然后求出一些点的坐标.连接
轴,建立空间直角坐标系,然后求出一些点的坐标.连接![]() ,可说明
,可说明![]() 为平面ACFD的一条法向量,设平面
为平面ACFD的一条法向量,设平面![]() 的法向量为
的法向量为![]()
根据![]() 即可求出法向量
即可求出法向量![]() ,设平面
,设平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,根据
,根据![]() 即可求出平面
即可求出平面![]() 与平面
与平面![]() 所成的角的大小.
所成的角的大小.
证明:
在三棱台DEF-ABC中,
由BC=2EF,H为BC的中点,
可得BH∥EF,BH=EF,
所以四边形BHFE为平行四边形,
可得BE∥HF.在△ABC中,G为AC的中点,H为BC的中点,所以GH∥AB.
又GH∩HF=H,
所以平面FGH∥平面ABED.
因为BD平面ABED,
所以BD∥平面FGH.
(2)解 设AB=2,则CF=1.

在三棱台DEF-ABC中,G为AC的中点,由DF=![]() AC=GC,可得四边形DGCF为平行四边形,
AC=GC,可得四边形DGCF为平行四边形,
因此DG∥FC,又FC⊥平面ABC,所以DG⊥平面ABC.
在△ABC中,由AB⊥BC,∠BAC=45°,G是AC中点.所以AB=BC,GB⊥GC,
因此GB,GC,GD两两垂直.以G为坐标原点,
建立如图所示的空间直角坐标系G-xyz.
所以G(0,0,0),B(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),D(0,0,1).
,0),D(0,0,1).
可得H![]() ,F(0,
,F(0,![]() ,1),
,1),
故![]() =
=![]() ,
,![]() =(0,
=(0,![]() ,1).
,1).
设n=(x,y,z)是平面FGH的一个法向量,
则由 可得
可得![]()
可得平面FGH的一个法向量n=(1,-1,![]() ).
).
因为![]() 是平面ACFD的一个法向量,
是平面ACFD的一个法向量,![]() =(
=(![]() ,0,0).
,0,0).
所以cos〈![]() ,n〉=
,n〉=![]() =
=![]() =
=![]() .
.
所以平面FGH与平面ACFD所成角(锐角)的大小为60°.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
