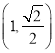题目内容
【题目】已知抛物线![]() 的顶点在坐标原点
的顶点在坐标原点![]() ,过抛物线
,过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 与该抛物线交于
与该抛物线交于![]() 两点,
两点, ![]() 面积的最小值为2.
面积的最小值为2.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)试问是否存在定点![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,当
两点,当![]() 三点不共线时,使得以
三点不共线时,使得以![]() 为直径的圆必过点
为直径的圆必过点![]() .若存在,求出所有符合条件的点;若不存在,请说明理由.
.若存在,求出所有符合条件的点;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)第(1)问,通过利用函数的思想研究![]() 面积的最小值得到关于P方程,解方程即可. (2)第(2)问,根据以
面积的最小值得到关于P方程,解方程即可. (2)第(2)问,根据以![]() 为直径的圆必过点
为直径的圆必过点![]() 得到
得到![]() 0,
0,
化简得到m和k的关系,看是否满足题意.
试题解析:
(1)设直线的方程为![]() ,设
,设![]() ,
,
联立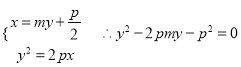
![]() 面积的最小即
面积的最小即![]() 最小,
最小,
![]()
所以当m=0时, ![]() 最小为2p,△MON面积的最小,
最小为2p,△MON面积的最小,
所以![]()
(2)假设存在这样的定点![]() ,当
,当![]() 不垂直于
不垂直于![]() 轴时,可设直线为
轴时,可设直线为![]() ,显然
,显然![]() .
.
联立可得![]() ,由于p=2,所以点
,由于p=2,所以点![]() .
.
设![]() ,则
,则![]() ,
, ![]() ,
,

化简可得![]() ,即
,即![]()
当![]() 时,
时, ![]() ,恒过定点
,恒过定点![]() ,即为点A,不合题意;
,即为点A,不合题意;
当![]() 时,
时, ![]() ,恒过定点
,恒过定点![]() ,此时存在定点满足条件.
,此时存在定点满足条件.
容易验证当直线过点![]() 且垂直于
且垂直于![]() 轴时,
轴时, ![]() ,综上,存在唯一定点
,综上,存在唯一定点![]() 满足条件.
满足条件.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案【题目】《中国好声音(![]()
![]()
![]()
![]() )》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
)》是由浙江卫视联合星空传媒旗下灿星制作强力打造的大型励志专业音乐评论节目,于2012年7月13日在浙江卫视播出.每期节目有四位导师参加.导师背对歌手,当每位参赛选手演唱完之前有导师为其转身,则该选手可以选择加入为其转身的导师的团队中接受指导训练.已知某期《中国好声音》中,6位选手唱完后,四位导师为其转身的情况如下表所示:
导师转身人数(人) | 4 | 3 | 2 | 1 |
获得相应导师转身的选手人数(人) | 1 | 2 | 2 | 1 |
现从这6位选手中随机抽取两人考查他们演唱完后导师的转身情况.
(1)求选出的两人导师为其转身的人数和为4的概率;
(2)记选出的2人导师为其转身的人数之和为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了![]() 名男生、
名男生、![]() 名女生进行为期一周的跟踪调查,调查结果如表所示:
名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为学生使用手机的时间长短与性别有关?
的前提下认为学生使用手机的时间长短与性别有关?
(2)在这![]() 名女生中,调查小组发现共有
名女生中,调查小组发现共有![]() 人使用国产手机,在这
人使用国产手机,在这![]() 人中,平均每天使用手机不超过
人中,平均每天使用手机不超过![]() 小时的共有
小时的共有![]() 人.从平均每天使用手机超过
人.从平均每天使用手机超过![]() 小时的女生中任意选取
小时的女生中任意选取![]() 人,求这
人,求这![]() 人中使用非国产手机的人数
人中使用非国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: 
![]()