题目内容
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]() .
.
【解析】
(1)先证明平面![]() 平面
平面![]() ,再证明
,再证明![]() 平面
平面![]() ;(2)分别以
;(2)分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立空间直角坐标系,利用向量法求异面直线
轴的非负半轴,建立空间直角坐标系,利用向量法求异面直线![]() 和
和![]() 所成角;(3)设
所成角;(3)设![]() ,
,![]() ,利用向量法得到
,利用向量法得到![]() ,解方程即得t的值和
,解方程即得t的值和![]() 的长.
的长.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∵平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
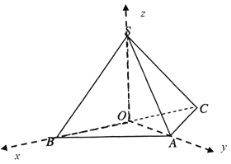
如图,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立空间直角坐标系,
轴的非负半轴,建立空间直角坐标系,
∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵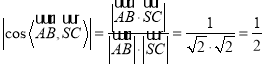 ,
,
∴异面直线![]() 和
和![]() 所成角为
所成角为![]() .
.
(3)设![]() 为平面
为平面![]() 的法向量,
的法向量,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∵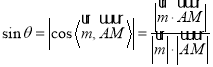 ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (舍),
(舍),![]() ,
,
∴![]() 的长为
的长为![]() .
.

【题目】随着节能减排意识深入人心以及共享单车在饶城的大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车。为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果认为每周使用超过3次的用户为“喜欢骑行共享单车”,请完成![]() 列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
列表(见答题卡),并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关?
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,视频率为概率,在我市所有“骑行达人”中,随机抽取4名用户.
① 求抽取的4名用户中,既有男生“骑行达人”又有女“骑行达人”的概率;
②为了鼓励女性用户使用共享单车,对抽出的女“骑行达人”每人奖励500元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式: 
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


