题目内容
三棱锥P-ABC中,AP=AC,PB=2,将此三棱锥沿三条侧棱剪开,其展开图是一个直角梯形p1p2p3A,如图.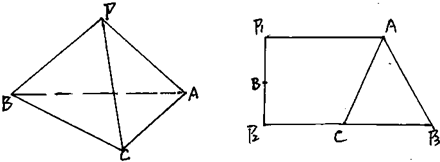
(1)求证:PB⊥AC
(2)求PB与面ABC所成角的大小.
(3)(只理科做)求三棱锥P-ABC外接球的面积.

(1)求证:PB⊥AC
(2)求PB与面ABC所成角的大小.
(3)(只理科做)求三棱锥P-ABC外接球的面积.
(1)证明:由展开图知:P1B⊥P1A,P2B⊥P2C
∴BP⊥PC,BP⊥PA,∴BP⊥平面PAC
∵AC?平面PAC,∴PB⊥AC
(2)设PA=AC=AP3=x,P3C=y
作AE⊥CP3,则E为CP3的中点
∴x2-(
)2=16,且x=y+
,解得 x=3
,y=2
即PA=AC=3
,PC=2
作PO⊥平面ABC,连接BO交AC于D,连接PD
∴∠PBO为PB与面ABC所成角
∵BP⊥平面PAC,易证AC⊥BD,AC⊥PD
在△PAC中,
×2
×4=
×3
×PD
∴PD=
∴tan∠PBO=
=
,
∴∠PBO=arctan
(3)设△PAC的外接圆圆心为Q,球心为O.连接PQ并延长交球面于M,连BM,OQ
∵BP⊥平面PAC,OQ⊥平面PAC,∴BP∥OQ
∴平面BPM是球的一个大圆
在△BPM中,BP=2,PM=
∴BM=
=
,∴球半径R=
∴球的表面积S=4πR2=

∴BP⊥PC,BP⊥PA,∴BP⊥平面PAC
∵AC?平面PAC,∴PB⊥AC
(2)设PA=AC=AP3=x,P3C=y
作AE⊥CP3,则E为CP3的中点
∴x2-(
| y |
| 2 |
| y |
| 2 |
| 2 |
| 2 |
即PA=AC=3
| 2 |
| 2 |
作PO⊥平面ABC,连接BO交AC于D,连接PD
∴∠PBO为PB与面ABC所成角
∵BP⊥平面PAC,易证AC⊥BD,AC⊥PD
在△PAC中,
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴PD=
| 8 |
| 3 |
∴tan∠PBO=
| PD |
| PB |
| 4 |
| 3 |
∴∠PBO=arctan
| 4 |
| 3 |
(3)设△PAC的外接圆圆心为Q,球心为O.连接PQ并延长交球面于M,连BM,OQ
∵BP⊥平面PAC,OQ⊥平面PAC,∴BP∥OQ
∴平面BPM是球的一个大圆
在△BPM中,BP=2,PM=
| 9 |
| 2 |
∴BM=
22+(
|
| ||
| 2 |
| ||
| 4 |
∴球的表面积S=4πR2=
| 97π |
| 4 |

练习册系列答案
相关题目