题目内容

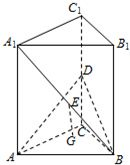
如图，在三棱柱ABC-A1B1C1中，AC=BC=CC1∠ACB=90°，CC1⊥平面ABC，则AC1与平面ABB1A1所成角的大小为______．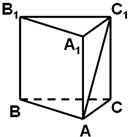
取B1C1的中点D，连接AD，C1D，如图所示

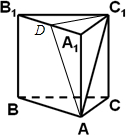
易得在△A1B1C1中，C1D⊥A1B1，又由AA1⊥C1D，
易得C1D⊥平面A1B1BA，
∴C1D⊥AD
则∠C1AD即为AC1与平面ABB1A1所成角的大小
在Rt△C1AD中，CD=
1
2
C1A
即sin∠C1AD=
1
2

∴∠C1AD=30°
故AC1与平面ABB1A1所成角的大小为30°
故答案为：30°
练习册系列答案
相关题目
如图，在正方体ABCD-A1B1C1D1中，E，F，G，H分别为AA1，AB，BB1，B1C1的中点，则异面直线EF与GH所成的角等于______．
已知四棱柱ABCD-A1B1C1D1，侧棱与底面垂直，底面ABCD是菱形且∠BAD=60°，侧棱与底面边长均为2，则面AB1C与底面A1B1C1D1，ABCD所成角的正弦值为（　　）
A．
1
2
B．2C．
5
5
D．
2
5
5
三棱锥P-ABC中，AP=AC，PB=2，将此三棱锥沿三条侧棱剪开，其展开图是一个直角梯形p1p2p3A，如图．
（1）求证：PB⊥AC
（2）求PB与面ABC所成角的大小．
（3）（只理科做）求三棱锥P-ABC外接球的面积．
已知正方体ABCD-A1B1C1D1，则直线AB与平面BDA1所成角的正弦值等于______．
如图，边长为2的正方形A1ACC1绕直线CC1旋转90°得到正方形B1BCC1，D为CC1的中点，E为A1B的中点，G为△ADB的重心．
（1）求直线EG与直线BD所成的角；
（2）求直线A1B与平面ADB所成的角的正弦值．
在正方体ABCD-A1B1C1D1中，直线A1B和平面ABCD所成角是______．
在正方体ABCD-A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值构成的集合是（　　）
A．{t|
2
5
5
≤t≤2
3
}		B．{t|
2
5
5
≤t≤2}		C．{t|2≤t≤2
3
}		D．{t|2≤t≤2
2
}
如图，在三棱锥P-ABC中，PB⊥面ABC，∠ABC=90°，AB=BC=2，∠PAB=45°，点D，E，F分别是AC，AB，BC的中点．
（1）求证：EF⊥PD；
（2）求直线PF与平面PBD所成的角的大小；
（3）求二面角E-PF-B的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网