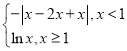题目内容
【题目】函数![]() ,
,![]() ,
,![]() .
.
(1)设![]() ,假设
,假设![]() 在
在![]() 上递减,求
上递减,求![]() 的取值范围;
的取值范围;
(2)假设![]() ,求证:
,求证:![]() .
.
(3)是否存在实数![]() ,使得
,使得![]() 恒成立,假设存在,求出
恒成立,假设存在,求出![]() 的取值范围,假设不存在,请说明理由.
的取值范围,假设不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在实数
;(2)见解析;(3)存在实数![]()
【解析】
(1)由![]() 在
在![]() 递减,得
递减,得![]() 在
在![]() 恒成立,
恒成立, ![]() ,即可得到本题答案;
,即可得到本题答案;
(2)要证明![]() 时,
时,![]() ,只需证明当
,只需证明当![]() ,
,![]() ,算出
,算出![]() 的最小值和
的最小值和![]() 的最大值,即可得到本题答案;
的最大值,即可得到本题答案;
(3)分![]() 和
和![]() 考虑
考虑![]() 的最小值,即可得到本题答案.
的最小值,即可得到本题答案.
(1)![]() ,
,![]() ,
,
由![]() 在
在![]() 递减,得
递减,得![]() 在
在![]() 恒成立,所以
恒成立,所以![]() ,
,
即![]() ,而
,而![]() ,当且仅当
,当且仅当![]() 时,等号成立,因此
时,等号成立,因此![]() ,
,
即![]() 的取值范围是
的取值范围是![]() ;
;
(2)要证明![]() 时,
时,![]() ,只需证明当
,只需证明当![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,得
,得![]()
当![]() 时,
时,![]() ,
,![]() 递减,
递减,
当![]() 时,
时,![]() ,
,![]() 递增,
递增,
因此![]() ,
,
![]() ,令
,令![]() ,解得
,解得![]()
当![]() 时,
时,![]() 递增,当
递增,当![]() 时,
时,![]() 递减,因此
递减,因此![]() ,而
,而![]() ,
,![]() ,因此
,因此![]() 成立,即
成立,即![]() 时,
时,![]() ;
;
(3)![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上递减,因此
上递减,因此![]()
假设![]() 恒成立,那么
恒成立,那么![]() ,即
,即![]() ,与
,与![]() 矛盾;
矛盾;
②当![]() 时,令
时,令![]() ,得
,得![]() .
.
1.当![]() 时,即
时,即![]() ,当
,当![]() 时,
时,![]() 递减,当
递减,当![]() 时,
时,![]() 递增,因此,当
递增,因此,当![]() 时,
时,![]() 取到唯一的极值,又是极小值,因此
取到唯一的极值,又是极小值,因此![]() .
.
假设![]() 恒成立,即
恒成立,即![]() ,解得
,解得![]() .
.
2.当![]() 时,即
时,即![]() ,当
,当![]() 时,
时,![]() 递减,因此
递减,因此![]() ,
,
假设![]() 恒成立,那么
恒成立,那么![]() ,即
,即![]() ,与
,与![]() 矛盾.
矛盾.
综上,存在实数![]() ,使得
,使得![]() 恒成立.
恒成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
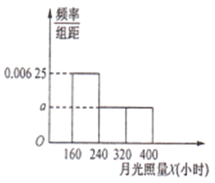
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取![]() 名学生的物理成绩(百分制)作为样本,按成绩分成5组:
名学生的物理成绩(百分制)作为样本,按成绩分成5组:![]() ,频率分布直方图如图所示,成绩落在
,频率分布直方图如图所示,成绩落在![]() 中的人数为20.
中的人数为20.

男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(1)求![]() 和
和![]() 的值;
的值;
(2)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数
和中位数![]() ;
;
(3)成绩在80分以上(含80分)为优秀,样本中成绩落在![]() 中的男、女生人数比为1:2,成绩落在
中的男、女生人数比为1:2,成绩落在![]() 中的男、女生人数比为3:2,完成
中的男、女生人数比为3:2,完成![]() 列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
列联表,并判断是否所有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:
| 0.50 | 0.05 | 0.025 | 0.005 |
| 0.455 | 3.841 | 5.024 | 7.879 |