题目内容
【题目】已知函数f(x)=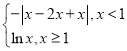 ,若对于t∈R,f(t)≤kt恒成立,则实数k的取值范围是________.
,若对于t∈R,f(t)≤kt恒成立,则实数k的取值范围是________.
【答案】[![]() ,1]
,1]
【解析】
本题条件“t∈R,f(t)≤kt”的几何意义是:在(-∞,+∞)上,函数y=f(t)的图像恒在直线y=kt的下方,利用数形结合的方法解决本问题.
令y=x3-2x2+x,x<1,则y′=3x2-4x+1=(x-1)·(3x-1),
令y′>0,即(x-1)(3x-1)>0,解得x<![]() 或x>1.又因为x<1,所以x<
或x>1.又因为x<1,所以x<![]() .
.
令y′<0,得![]() <x<1.
<x<1.
所以y的增区间是(-∞![]() ),减区间是(
),减区间是(![]() ,1),所以y极大值=
,1),所以y极大值=![]() .
.
根据图像变换可作出函数y=-|x3-2x2+x|,x<1的图像.
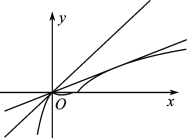
又设函数y=lnx(x≥1)的图像经过原点的切线斜率为k1,切点(x1,lnx1),
因为y′=![]() ,所以k1=
,所以k1=![]() =
=![]() ,解得x1=e,所以k1=
,解得x1=e,所以k1=![]() .
.
函数y=x3-2x2+x在原点处的切线斜率k2=y′x=0=1.
因为t∈R,f(t)≤kt,所以根据f(x)的图像,数形结合可得![]() ≤k≤1.
≤k≤1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目