题目内容
在抛物线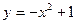
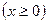上找一点P
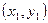，其中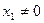
，过点P作抛物线的切线，使此切线与抛物线及两坐标轴所围平面图形的面积最小 （ ）
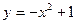
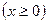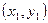上找一点P，其中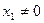，过点P作抛物线的切线，使此切线与抛物线及两坐标轴所围平面图形的面积最小 （ ）A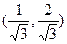． | B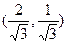． | C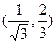． | D． |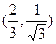
C；
由于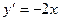
，因此过点P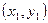的切线方程为
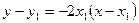，该切线与
，
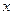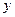轴的交点分别是
，
.
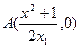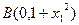所求面积A=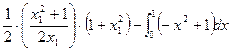
=
.
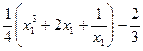
令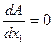
．(由于
)得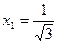
，
由于此问题的最小值存在，且在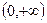
内有唯一驻点，
故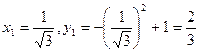
就是所求的点P，
即：取切点为P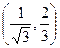
时，所求的图形面积最小．
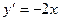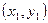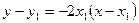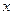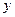，因此过点P的切线方程为，该切线与，轴的交点分别是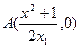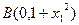，.所求面积A=
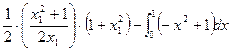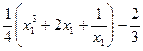
=.令
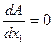．(由于)得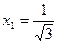， 由于此问题的最小值存在，且在
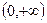内有唯一驻点，故
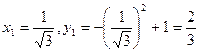就是所求的点P，即：取切点为P
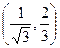时，所求的图形面积最小．
练习册系列答案
相关题目
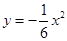的准线方程为 。
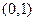与抛物线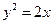
有且只有一个公共点的直线的条数是( )
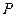到点
的距离比它到直线
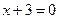的距离小1,则点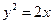
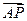=l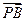
,l＞0,其中点P坐标为(0,1),
=
＋
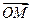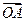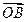,O为坐标原点.
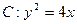，直线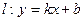
与C交于A，B两点，O为坐标原点。
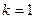，且直线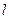
过抛物线C的焦点时，求
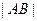的值；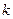
，
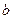之间满足的关系式，并证明直线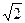
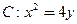上一点P到定点A（0，1）的距离为2，则点P到